Uma motocicleta foi vendida com um lucro de 25% sobre o preço de custo.Entretanto,se tivesse sido calculado sobre o preço de venda,teria o vendedor ganho R$ 1.000,00 a mais.Qual o preço de venda e qual o preço de custo da motocicleta?
Ja tenteni muita coisa gente mas ta dificil me ajudem por favor abraçosss


 ao preço de custo.
ao preço de custo.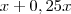 , ou seja,
, ou seja, 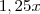 .
.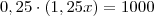 . Resolvendo esta equação temos que
. Resolvendo esta equação temos que 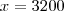 .
.
