por favor ajuda a resolver essas questões:
1) Três números inteiros distintos de -20 a 20 foram escolhidos de forma que seu produto seja um número negativo. O número de maneiras diferentes de se fazer essa escolha é:
2) Quantos anagramas com 4 letras distintas podemos formar com as 10 primeiras letras do alfabeto e que contenham 2 das letras a,b e c?
3) As matrizes A= (aij)4X4 E B= (bij)4x4 são tais que 2aij=3bij. Se o determinante da matriz A é igual a 3/4, então o determinante da matriz B é igual a:



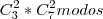 . Como os anagramas são as permutações das 4 letras escolhidas, o número de anagramas é:
. Como os anagramas são as permutações das 4 letras escolhidas, o número de anagramas é: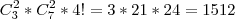

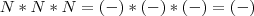
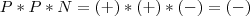 , mas aqui temos três situações a saber, veja:
, mas aqui temos três situações a saber, veja: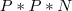 ou
ou 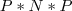 ou
ou 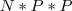 , portanto:
, portanto: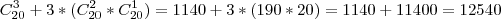
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)