-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477771 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528885 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492434 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 697298 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2106507 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por valleska » Seg Mai 18, 2009 21:46
por valleska » Seg Mai 18, 2009 21:46
Alguém pode me ajudar... to tentando resolver esse exercício, disseram p/ usar teorema das linhas, só q não consigo desenvolver a questão...
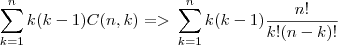
-
valleska
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Mai 16, 2009 00:11
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Téc. Laboratório
- Andamento: formado
Voltar para Desafios Enviados
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quantidade de números de linhas
por leticiapires52 » Qui Mai 29, 2014 12:41
- 2 Respostas
- 3418 Exibições
- Última mensagem por leticiapires52

Sex Mai 30, 2014 10:46
Progressões
-
- Forma Escada Reduzida por Linhas
por ricardotdai » Seg Abr 19, 2010 03:24
- 2 Respostas
- 4112 Exibições
- Última mensagem por ricardotdai

Ter Abr 20, 2010 01:25
Matrizes e Determinantes
-
- Trigonometria (Relações entre linhas trigonométricas)
por claudia » Seg Ago 25, 2008 14:58
- 5 Respostas
- 5136 Exibições
- Última mensagem por claudia

Qua Ago 27, 2008 17:15
Trigonometria
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4131 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3049 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
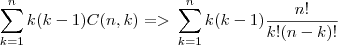


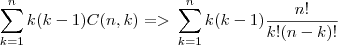

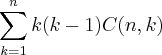
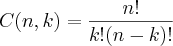
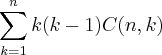 =
= 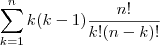


 .
.
 :
: