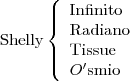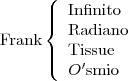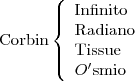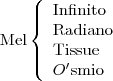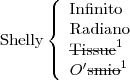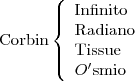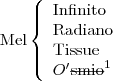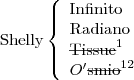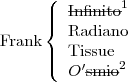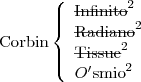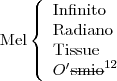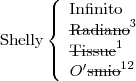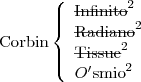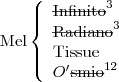-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478704 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534731 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498330 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 714081 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2136271 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Neperiano » Qui Jun 19, 2008 16:48
por Neperiano » Qui Jun 19, 2008 16:48
Eu não sei se eu posso fazer isso mas vou fazer irei postar umonte de perguntas sobre logica aqui.
1: Imagine um campo de 1 KM de comprimento por 1 KM de largura, num dia qualquer um homem vai bem no meio desse terreno e planta uma semente. No outro dia ela começa a crescer, e a partir dai todo o dia ele sempre cresce o dobro dela mesma. Se em 30 dias o campo esta todo coberto por essa planta, em quantos dias o campo estava coberto por metade dessa planta?
a - 15
b - 2
c - 3
d - 20
e - NDA
2: Qual dos cinco faz a melhor comparação?
CAACCAC está para 3113313 como CACAACAC está para:
a - 13133131
b - 13133313
c - 31311131
d - 31311313
e - 31313113
Respostas:
Pergunte para mim
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Qui Jun 19, 2008 17:51
por Molina » Qui Jun 19, 2008 17:51
1) E
explicação: pois supomos que no primeiro dia ela cresceu
x, no dia seguinte o dobro, ou seja,
2x, no outro o dobro novamente, ou seja,
2*2x = 4x, e assim sucessivamente, até chegar no dia 30, entao teria este aspecto:
dia 1: x
dia 2: 2x
dia 3: 2*(2x) =

dia 3: 2*(2*2x) =
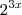
...
dia 29:

dia 30:

disto temos que

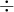

=

ou seja, no 29° dia.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Qui Jun 19, 2008 17:55
por Molina » Qui Jun 19, 2008 17:55
2) D - 31311313
juro que fiquei um bom tempo procurando uma "pegadinha" nesta questão, mas não encontrei, então, eu colocaria esta alternativa. confirma depois se as respostas estão certas ou erradas.
abraços
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Sex Jun 20, 2008 14:09
por Neperiano » Sex Jun 20, 2008 14:09
Acertou todas, tambem essas tavam facil, vou colocar umas dificeis agora.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Neperiano » Sex Jun 20, 2008 14:11
por Neperiano » Sex Jun 20, 2008 14:11
Acertou todas, tambem essas tavam facil, vou colocar umas dificeis agora.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Neperiano » Sex Jun 20, 2008 14:19
por Neperiano » Sex Jun 20, 2008 14:19
Travessia de jangada
Imagine esta situação: Existem 8 pessoas a querer atravessar um rio, um pai, uma mãe e dois filhos, duas filhas, um policial e um prisioneiro, e apenas dispõem de uma jangada que suporta unicamente duas pessoas de cada vez.
Analisando o problema, deparamos que:
Os únicos que sabem manobrar a jangada são: o pai, a mãe, e o policial;
Os filhos não suportam a mãe na ausência do pai;
As filhas, por sua vez, não suportam o pai na ausência da mãe;
O prisioneiro é demasiado perigoso para estar sozinho com qualquer membro da família;
Como já dissemos, a jangada só suporta duas pessoas de cada vez.
Consegue encontrar a solução?
Quatro cientistas:
Quatro cientistas sentam-se a jantar. Os nomes são Shelly, Frank, Corbin e Mel. Os quatro colocam cartas na mesa com apenas os seus apelidos: Infinito, Radiano, Tissue, e Ósmio. Será capaz de descobrir os nomes completos dos cientistas, sabendo apenas que:
Nenhum cientista tem um apelido em que apareça a inicial do primeiro nome;
O apelido de Corbin é também um elemento;
O primeiro nome de Radiano contém um R;
Soma=Produto
Consegue determinar quais os dois números cujo resultado, quando multiplicados entre si, é igual ao resultado da sua soma? E outro par?
Se um dos dois números é três, o outro número é _____? Fracções são permitidas.
Agora, consegue encontrar três números diferentes cujo resultado, quando multiplicados entre si, é igual à sua soma? Não são permitidas fracções.
Estas estão dificeis
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sex Jun 20, 2008 17:32
por Molina » Sex Jun 20, 2008 17:32
Soma=Produto
Consegue determinar quais os dois números cujo resultado, quando multiplicados entre si, é igual ao resultado da sua soma? E outro par?
0 + 0 = 0
0 * 0 = 0
2 + 2 = 4
2 * 2 = 4
Se um dos dois números é três, o outro número é _____? Fracções são permitidas.
3 * A = 3 + A
3 * A - 3 - A = 0
A * (3 - 1) - 3 = 0
A * 2 - 3 = 0
A * 2 = 3
A = 3/2
Agora, consegue encontrar três números diferentes cujo resultado, quando multiplicados entre si, é igual à sua soma? Não são permitidas fracções.
1 + 2 + 3 = 1 * 2 * 3
0 + n - n = 0 * n * (-n)
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Sex Jun 20, 2008 20:01
por Neperiano » Sex Jun 20, 2008 20:01
Acertou, agora quero ver fazer as outras duas questões
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por admin » Sex Jun 20, 2008 21:20
por admin » Sex Jun 20, 2008 21:20
Considerando que o "nome completo" seja "nome+apelido", então:
Shelly Infinito
Frank Radiano
Corbin Ósmio
Mel Tissue
Vou comentar meu procedimento...
Numerei as hipóteses:
1: Nenhum cientista tem um apelido em que apareça a inicial do primeiro nome;
2: O apelido de Corbin é também um elemento;
3: O primeiro nome de Radiano contém um R.
Então, inicialmente, estas são as possibilidades:
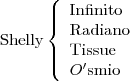
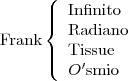
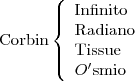
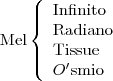
Farei as eliminações em etapas, tachando os apelidos, justificando com o número da hipótese.
Primeira eliminação:
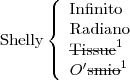

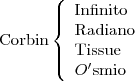
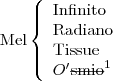
Segunda eliminação:
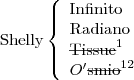
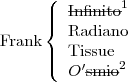
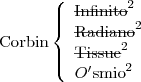
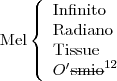
Terceira eliminação:
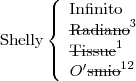

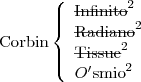
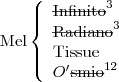
Os nomes ficam formados pelas possibilidades restantes.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 886
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Neperiano » Sáb Jun 21, 2008 12:52
por Neperiano » Sáb Jun 21, 2008 12:52
Acertou agora quero ver fazerem a primeira questão
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sáb Jun 21, 2008 13:07
por Molina » Sáb Jun 21, 2008 13:07
Maligno escreveu:Acertou, agora quero ver fazer as outras duas questões
Opa.
As outras 2 questões eu ja conhecia,
então prefiro deixar pra alguem que nunca
tenha visto.
Caso demore, eu começo a solução.
Abraços.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Sáb Jun 21, 2008 13:26
por Neperiano » Sáb Jun 21, 2008 13:26
Oh molina e fabio vcs tem MSN ou coisa assim, pra conversar com voces?
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por admin » Sáb Jun 21, 2008 14:12
por admin » Sáb Jun 21, 2008 14:12
Olá Maligno!
Assim como o Molina, eu também já havia feito o outro problema, inclusive tem um outro parecido mais simples, com galinha, raposa e milho.
Eu quase não fico online no Messenger, mas depois adiciono ao meu perfil.
Abraços!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 886
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Neperiano » Sáb Jun 21, 2008 14:13
por Neperiano » Sáb Jun 21, 2008 14:13
Então vamos deixar ele aqui para outra pessoa tentar resolver.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sáb Jun 21, 2008 17:25
por Molina » Sáb Jun 21, 2008 17:25
Maligno escreveu:Oh molina e fabio vcs tem MSN ou coisa assim, pra conversar com voces?
Eu também entro raramente no MSN.
É mais fácil me encontrar no Google Talk.
Se você tiver, adiciona:
d0md13g0@gmail.comabr.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Sáb Jun 21, 2008 19:41
por Neperiano » Sáb Jun 21, 2008 19:41
não tenho, mas azar então vamos conversar por aqui mesmo
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por admin » Sáb Jun 21, 2008 20:40
por admin » Sáb Jun 21, 2008 20:40
Ainda pretendo disponibilizar um chat aqui na Ajuda Matemática.
Na ocasião, todos serão notificados via newsletter.
Abraços!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 886
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Neperiano » Sex Nov 11, 2011 15:51
por Neperiano » Sex Nov 11, 2011 15:51
Ola
Vou repostar uma questão que não foi resolvida, e mais uma que eu lembrei agora:
1) Travessia de jangada
Imagine esta situação: Existem 8 pessoas a querer atravessar um rio, um pai, uma mãe e dois filhos, duas filhas, um policial e um prisioneiro, e apenas dispõem de uma jangada que suporta unicamente duas pessoas de cada vez.
Analisando o problema, deparamos que:
Os únicos que sabem manobrar a jangada são: o pai, a mãe, e o policial;
Os filhos não suportam a mãe na ausência do pai;
As filhas, por sua vez, não suportam o pai na ausência da mãe;
O prisioneiro é demasiado perigoso para estar sozinho com qualquer membro da família;
Como já dissemos, a jangada só suporta duas pessoas de cada vez.
Consegue encontrar a solução?
2) Travessia do rio
Há 3 missionário e 3 indios de um lado do rio, todos precisam atravessar o rio através de uma balsa. A balsa pode levar 1 ou 2 pessoas de um lado para outro. Sabendo que não podem ficar mais indios do que missionários nos lados do rio e na balsa, determinie como é possível resolver este problema.
Quero ver quem é bom mesmo
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Desafios Enviados
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LÓGICA] simplificação lógica e leis de equivalência
por MatheusComp606 » Qua Ago 24, 2016 16:13
- 1 Respostas
- 4872 Exibições
- Última mensagem por adauto martins

Seg Ago 29, 2016 15:34
Lógica
-
- lÓGICA
por Jaison Werner » Qui Set 15, 2011 11:28
- 2 Respostas
- 3052 Exibições
- Última mensagem por Neperiano

Qui Nov 10, 2011 15:31
Lógica e Conjuntos
-
- Lógica
por Pstefani » Ter Set 20, 2011 19:56
- 1 Respostas
- 2157 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 21:40
Sistemas de Equações
-
- [lógica]
por Ed_29 » Qui Ago 09, 2012 21:25
- 5 Respostas
- 6363 Exibições
- Última mensagem por fraol

Sáb Ago 11, 2012 16:09
Conjuntos
-
- Logica
por RafahAparecida » Ter Out 16, 2012 18:16
- 1 Respostas
- 1749 Exibições
- Última mensagem por MarceloFantini

Ter Out 16, 2012 18:54
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




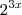



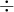
 =
=