Indeterminações
Enviado: Sex Nov 27, 2009 19:23Olá Pessoa!
Estou começando a colecionar questões que possam ferrar alunos. Sendo assim, gostaria de uma ajuda de vcs. Tenho uma questão: Quero saber todas as formas possíveis para a solução desta indeterminação:
![\lim_{x \to 2} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}}](/latexrender/pictures/6cb7b0b9898bd1a29405699072c2dbb9.png "\lim_{x \to 2} \frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}}")
Estou começando a colecionar questões que possam ferrar alunos. Sendo assim, gostaria de uma ajuda de vcs. Tenho uma questão: Quero saber todas as formas possíveis para a solução desta indeterminação:
![\frac{\sqrt{x-2}}{\sqrt[3]{x²-4}}=\frac{\sqrt{x-2}}{\sqrt[3]{(x-2)*(x+2)}}=\frac{\sqrt{x-2}}{\sqrt[3]{x-2}*\sqrt[3]{x+2}} =\frac{{(x-2)}^{\frac{1}{6}}}{\sqrt[3]{x+2}} = \frac{0}{\sqrt[3]{4}} = 0](/latexrender/pictures/e3cfc1351020cd8a7d8c29afd4ad4a78.png "\frac{\sqrt{x-2}}{\sqrt[3]{x²-4}}=\frac{\sqrt{x-2}}{\sqrt[3]{(x-2)*(x+2)}}=\frac{\sqrt{x-2}}{\sqrt[3]{x-2}*\sqrt[3]{x+2}} =\frac{{(x-2)}^{\frac{1}{6}}}{\sqrt[3]{x+2}} = \frac{0}{\sqrt[3]{4}} = 0")
![\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} = \frac{{e}^{\frac{ln(x-2)}{2}}}{{e}^{\frac{ln(x^2-4)}{3}}} = {e}^{\frac{ln(x-2)}{2}-\frac{ln(x^2-4)}{3}}} = {e}^{\frac{3ln(x-2)}{6}-\frac{2ln(x^2-4)}{6}}} = {e}^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{1}{6}*ln\left(\frac{(x-2)^3}{(x^2-4)^2}\right)} = e^{\frac{1}{6}*ln\left(\frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16}\right)}](/latexrender/pictures/fd56810d8924cc94867f3e9285aeaa00.png "\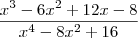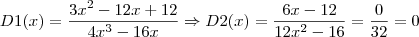frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} = \frac{{e}^{\frac{ln(x-2)}{2}}}{{e}^{\frac{ln(x^2-4)}{3}}} = {e}^{\frac{ln(x-2)}{2}-\frac{ln(x^2-4)}{3}}} = {e}^{\frac{3ln(x-2)}{6}-\frac{2ln(x^2-4)}{6}}} = {e}^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{ln((x-2)^3)}{6}-\frac{ln((x^2-4)^2)}{6}} = e^{\frac{1}{6}*ln\left(\frac{(x-2)^3}{(x^2-4)^2}\right)} = e^{\frac{1}{6}*ln\left(\frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16}\right)}")
![\sqrt[6]{\lim_{x \to 2} \left(\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \right)^6 } \right} = \sqrt[6]{ \lim_{x \to 2} \frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16} }](/latexrender/pictures/b0b8935e4f09b504eeb72fb27711db61.png "\sqrt[6]{\lim_{x \to 2} \left(\frac{\sqrt{x-2}}{\sqrt[3]{x^2-4}} \right)^6 } \right} = \sqrt[6]{ \lim_{x \to 2} \frac{x^3 - 6x^2 + 12x - 8}{x^4-8x^2 + 16} }")