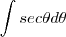-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480728 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542380 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 506105 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 735202 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2181807 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Pessoa Estranha » Dom Nov 17, 2013 21:59
por Pessoa Estranha » Dom Nov 17, 2013 21:59
Mostre que:
![\int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C \int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C](/latexrender/pictures/60f6baa45c752fc0e845aad793a1928b.png)
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Nov 17, 2013 23:06
por e8group » Dom Nov 17, 2013 23:06
Dica :
Observando identidade
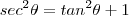
vemos que é possível realizar uma substituição trigonométrica
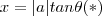
(desde que

) de modo obtermos outra integral mais simples . Se considerarmos

, podemos sempre escrever

sob a forma

para algum

em
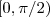
. Segue-se que
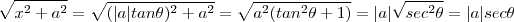
(pois
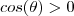
)
e derivando-se a expressão

,
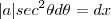
. Após esta substituição ,veja como a integral ficou mais simples de ser calculada :
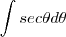
Agora tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Desafios Enviados
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [desafio] cálculo quem sabe?
por Rafael d » Seg Nov 18, 2013 19:15
- 0 Respostas
- 1212 Exibições
- Última mensagem por Rafael d

Seg Nov 18, 2013 19:15
Cálculo: Limites, Derivadas e Integrais
-
- Desafio! Questões de cálculo, Teor. da Divergência de Gauss
 por petdias » Sáb Ago 03, 2013 18:06
por petdias » Sáb Ago 03, 2013 18:06
- 0 Respostas
- 787 Exibições
- Última mensagem por petdias

Sáb Ago 03, 2013 18:06
Cálculo: Limites, Derivadas e Integrais
-
- Desafio
por Guarinense » Sex Nov 10, 2017 22:25
- 0 Respostas
- 5123 Exibições
- Última mensagem por Guarinense

Sex Nov 10, 2017 22:25
Teoria dos Números
-
- Desafio dos Dez Pontos
 por Molina » Sáb Jul 12, 2008 00:02
por Molina » Sáb Jul 12, 2008 00:02
- 6 Respostas
- 4740 Exibições
- Última mensagem por admin

Dom Jul 13, 2008 17:00
Desafios Fáceis
-
- Desafio de lógica
por Twister » Qua Ago 13, 2008 21:46
- 10 Respostas
- 9231 Exibições
- Última mensagem por andymath

Qua Mar 31, 2010 19:14
Desafios Enviados
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C \int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C](/latexrender/pictures/60f6baa45c752fc0e845aad793a1928b.png)


![\int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C \int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C](/latexrender/pictures/60f6baa45c752fc0e845aad793a1928b.png)

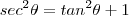 vemos que é possível realizar uma substituição trigonométrica
vemos que é possível realizar uma substituição trigonométrica 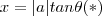 (desde que
(desde que  ) de modo obtermos outra integral mais simples . Se considerarmos
) de modo obtermos outra integral mais simples . Se considerarmos  , podemos sempre escrever
, podemos sempre escrever  sob a forma
sob a forma  para algum
para algum  em
em 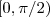 . Segue-se que
. Segue-se que 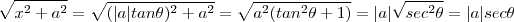 (pois
(pois 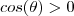 )
) ,
, 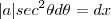 . Após esta substituição ,veja como a integral ficou mais simples de ser calculada :
. Após esta substituição ,veja como a integral ficou mais simples de ser calculada :