eu tenho que fazer assim:
o programa pede"Kilobit por segundo", e tamanho do arquivo em KB(kilobyte), e o programa de o tempo
o programa pede"Kilobit por segundo", e tamanho do arquivo em MB(megabyte), e o programa de o tempo
o programa pede"Kilobit por segundo", e tamanho do arquivo em GB(gigabyte), e o programa de o tempo
eu sei que, 1 kilobit é = a, 0.125KB e 0.0001220703125MB
e 1GB é = a 8388608Kilobit
OBS: note a diferença entre kilobite(Kb) e kilobyte(KB), um conversor de bit: http://www.gwebtools.com.br/converter-bit
vou postar uma foto do programa só para que entendam melhor, tem a segunda parte e vou precisar de formulas ai eu posto aqui pedindo ajuda porque sou uma negação com formula, enchi a folha do caderno e quase n fiz evolução

ali em Kbps tem tb MB mais isso vou deixar para depois que fizer com Kbps


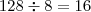 . Portanto, temos que 128 Kbps é equivalente a 16 KB/s.
. Portanto, temos que 128 Kbps é equivalente a 16 KB/s. . Portanto, temos que o tempo é de 7,5 segundos.
. Portanto, temos que o tempo é de 7,5 segundos.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.