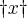 de x é definido como o maior número inteiro
de x é definido como o maior número inteiro 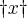 que é menor ou igual a x.
que é menor ou igual a x.Por exemplo
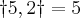 ;
; 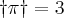 ;
; 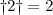 .
.Qual o valor da soma
![\dagger1\dagger +\dagger\sqrt[2]{2}\dagger + \dagger\sqrt[2]{3}\dagger+...+\dagger\sqrt[2]{200}\dagger \dagger1\dagger +\dagger\sqrt[2]{2}\dagger + \dagger\sqrt[2]{3}\dagger+...+\dagger\sqrt[2]{200}\dagger](/latexrender/pictures/76e66fd46dfd45020d68284f7fc07f0f.png) ?
?No começo eu fui somando os valores facilmente mas então percebi que perderia muito tempo já que esta questão caiu nas olímpiadas aqui da minha região. Como faço para resolvê-la?


 será sempre
será sempre  até chegarmos em
até chegarmos em  . Então, por exemplo
. Então, por exemplo  . Tente aplicar o mesmo raciocínio para outros intervalos. Existe uma forma de generalizar para os intervalos, procure.
. Tente aplicar o mesmo raciocínio para outros intervalos. Existe uma forma de generalizar para os intervalos, procure.

![\sqrt[2]{25} \sqrt[2]{25}](/latexrender/pictures/e4a5a0d745e039d5327ad2983233661c.png) basta irmos somando 5 até chegarmos no piso da
basta irmos somando 5 até chegarmos no piso da ![\sqrt[2]{36} \sqrt[2]{36}](/latexrender/pictures/12b047b03092656399d446e78440b0e3.png) e assim por diante.
e assim por diante.![\sqrt[2]{16} \sqrt[2]{16}](/latexrender/pictures/191ffcc471002d4e0ffc1c4a28bb655c.png) até
até ![\sqrt[2]{24} \sqrt[2]{24}](/latexrender/pictures/f3bc6e2a65dc93c241bc110261384a02.png) há 9 números(chamemos esse 9 de
há 9 números(chamemos esse 9 de 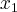 ).
).![\sqrt[2]{35} \sqrt[2]{35}](/latexrender/pictures/ee7a1b2b31c4e46cd16dd30e0467554e.png) há 11 números (seja
há 11 números (seja  , então
, então 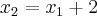 .
.![\sqrt[2]{48} \sqrt[2]{48}](/latexrender/pictures/e8f81210c3e7fee9992263cf368c5a14.png) há 13 números (
há 13 números (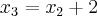 ). Então minha generalização é a seguinte :
). Então minha generalização é a seguinte : 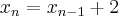
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
