-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478645 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534343 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 497922 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 713017 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2134379 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Aliocha Karamazov » Sex Set 09, 2011 01:25
por Aliocha Karamazov » Sex Set 09, 2011 01:25
Pessoal, vou postar nessa seção, pois esse exercício está no capítulo de sequência do livro...
Usando a propriedade arquimediana, prove que se

para todo

, então

-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por fraol » Sex Dez 16, 2011 19:05
por fraol » Sex Dez 16, 2011 19:05
Lá vai uma tentativa: (todo n Natural)

Se n tende a 0 então ficaremos com algo assim

o que é sempre verdade para qualquer

real e nada concluímos.
Se n tende ao

então ficaremos com

e portanto

.
É isso aí. Que tal?
Editado pela última vez por
fraol em Sáb Dez 17, 2011 06:16, em um total de 1 vez.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Sáb Dez 17, 2011 00:05
por MarceloFantini » Sáb Dez 17, 2011 00:05
Se fosse menor ou igual talvez, mas

não faz muito sentido.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Sáb Dez 17, 2011 06:13
por fraol » Sáb Dez 17, 2011 06:13
Oops!
Está certo Marcelo,
Vou repensar a tentativa, você tem alguma dica?
Abç,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Sáb Dez 17, 2011 20:53
por fraol » Sáb Dez 17, 2011 20:53
Repensando e usando melhor o enunciado, vamos a uma nova parcial:
(1) A propriedade Arquimediana diz que dados

tais que

então existe algum
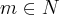
tal que

.
(2) Da hipótese do enunciado temos

, invertendo ficamos com

.
(3) Aplicando a Arquimediana em (2) pode-se, então, afirmar que existe algum
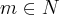
tal que

.
(4) Mas olhando para (3) e (1), vemos que o tal

em (3) só existirá se

E agora eu encalhei, será que foi a cerveja? Será que teremos que partir para uma contradição para provar a hipótese?
Bom, se alguém tiver alguma dica, por favor, manda pra cá.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Seg Dez 19, 2011 19:53
por fraol » Seg Dez 19, 2011 19:53
Retomando o raciocínio da minha intervenção anterior e, corrigindo alguns equívocos temos o seguinte:
(1) A propriedade Arquimediana diz que dados

tais que

então existe algum
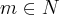
tal que

.
(2) Da hipótese do enunciado temos

. Vamos supor então que

e portanto

.
(3) Aplicando a Arquimediana em (2) pode-se, então, afirmar que existe algum
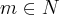
tal que

.
(4) Como

então

também, chamemos esse produto de

.
(5) Assim, chegamos a uma contradição:

e

. Ambos

e

naturais quaisquer contrariando a hipótese dada no enunciado original e a nossa suposição de que

.
(6) Portanto, só resta aceitar que

.
Aliás, há outra forma de forma provar isso. Antes teríamos que provar que o ínfimo do conjunto {

} é igual a 0 (usando a Arquimediana). E daí usaríamos limites, mas aí estaríamos usando outros recursos além da Arquimediana.
Demorou mas fechou.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Prove usando a Propriedade Arquimediana...] Propriedade Arq
por alessandro » Seg Abr 16, 2012 19:10
- 1 Respostas
- 1449 Exibições
- Última mensagem por alessandro

Seg Abr 16, 2012 19:12
Sequências
-
- Provar Propriedade Arquimediana
por Jovani Souza » Sáb Mai 18, 2013 12:32
- 1 Respostas
- 1655 Exibições
- Última mensagem por e8group

Sáb Mai 18, 2013 16:52
Sequências
-
- Funções - provar propriedade
por emsbp » Sáb Jul 07, 2012 17:59
- 2 Respostas
- 1389 Exibições
- Última mensagem por emsbp

Dom Jul 08, 2012 18:27
Funções
-
- Demonstre a propriedade
por Aliocha Karamazov » Sáb Jul 09, 2011 02:02
- 1 Respostas
- 1151 Exibições
- Última mensagem por Guill

Dom Jul 10, 2011 09:33
Funções
-
- Racionais: propriedade
por Victor Gabriel » Dom Mai 12, 2013 15:58
- 0 Respostas
- 1213 Exibições
- Última mensagem por Victor Gabriel

Dom Mai 12, 2013 15:58
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para todo
para todo  , então
, então 

 para todo
para todo  , então
, então 


 o que é sempre verdade para qualquer
o que é sempre verdade para qualquer  real e nada concluímos.
real e nada concluímos. então ficaremos com
então ficaremos com  e portanto
e portanto  .
.
 não faz muito sentido.
não faz muito sentido.


 tais que
tais que  então existe algum
então existe algum 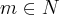 tal que
tal que  .
. , invertendo ficamos com
, invertendo ficamos com  .
. 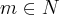 tal que
tal que  .
. em (3) só existirá se
em (3) só existirá se 

 tais que
tais que  então existe algum
então existe algum 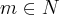 tal que
tal que  .
. . Vamos supor então que
. Vamos supor então que  e portanto
e portanto  .
.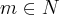 tal que
tal que  .
. então
então  também, chamemos esse produto de
também, chamemos esse produto de  .
. e
e  . Ambos
. Ambos  e
e  naturais quaisquer contrariando a hipótese dada no enunciado original e a nossa suposição de que
naturais quaisquer contrariando a hipótese dada no enunciado original e a nossa suposição de que  .
. .
.  } é igual a 0 (usando a Arquimediana). E daí usaríamos limites, mas aí estaríamos usando outros recursos além da Arquimediana.
} é igual a 0 (usando a Arquimediana). E daí usaríamos limites, mas aí estaríamos usando outros recursos além da Arquimediana.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.