-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477922 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529843 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493415 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 700042 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2111300 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Larissa28 » Dom Set 27, 2015 22:24
por Larissa28 » Dom Set 27, 2015 22:24
- - -- --
Editado pela última vez por
Larissa28 em Ter Set 29, 2015 18:51, em um total de 2 vezes.
-
Larissa28
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Mar 21, 2015 17:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Produção
- Andamento: cursando
 por adauto martins » Ter Set 29, 2015 15:39
por adauto martins » Ter Set 29, 2015 15:39
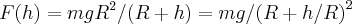
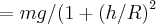
...
façamos
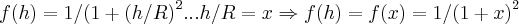
...
como sabemos:
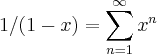
,entao teremos
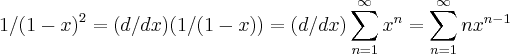
...logo teremos:
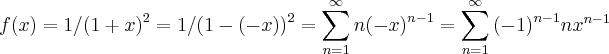
...voltando a F(h),teremos...
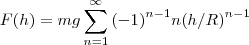
...
o raio é dado por
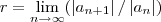
...entao
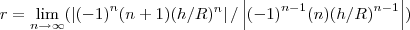

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Larissa28 » Ter Set 29, 2015 17:59
por Larissa28 » Ter Set 29, 2015 17:59
------
Editado pela última vez por
Larissa28 em Ter Set 29, 2015 18:51, em um total de 1 vez.
-
Larissa28
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Mar 21, 2015 17:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Produção
- Andamento: cursando
 por Larissa28 » Ter Set 29, 2015 18:00
por Larissa28 » Ter Set 29, 2015 18:00
-
Editado pela última vez por
Larissa28 em Ter Set 29, 2015 18:49, em um total de 1 vez.
-
Larissa28
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Mar 21, 2015 17:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Produção
- Andamento: cursando
 por adauto martins » Ter Set 29, 2015 18:16
por adauto martins » Ter Set 29, 2015 18:16
oi larissa...
eh eu costumo esquecer mesmo,qdo tenho q. usar esse editor,mas na igualdade seguinte R+h esta elevado ao quadrado...
e a resoluçao esta como devido...espero q. vc entenda...obrigado,e bons estudos...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Larissa28 » Ter Set 29, 2015 18:41
por Larissa28 » Ter Set 29, 2015 18:41
Muito obrigada (:
-
Larissa28
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Mar 21, 2015 17:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Produção
- Andamento: cursando
 por adauto martins » Ter Set 29, 2015 18:55
por adauto martins » Ter Set 29, 2015 18:55
ue pq vc retirou o enunciado...e ai entendeu a soluçao?...
depois resolva as outras,agora num vai dar,tbom...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qua Set 30, 2015 17:19
por adauto martins » Qua Set 30, 2015 17:19
ue larissa...cade as outras questoes de series q. vc postou,vc as retirou...pq?...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo 1] Manipulação de função
por Larissa28 » Ter Mar 24, 2015 23:54
- 2 Respostas
- 2228 Exibições
- Última mensagem por Larissa28

Qua Mar 25, 2015 19:47
Cálculo: Limites, Derivadas e Integrais
-
- Manipulação e Cálculo
por Jhenrique » Sex Dez 07, 2012 20:50
- 4 Respostas
- 4157 Exibições
- Última mensagem por Jhenrique

Seg Dez 17, 2012 12:51
Cálculo: Limites, Derivadas e Integrais
-
- [Manipulação de Proporções]
por Tatasacchi_123 » Seg Abr 08, 2013 13:12
- 1 Respostas
- 2220 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:04
Funções
-
- [Problema] Dificuldade com manipulação de fórmulas
 por FilipeMSoares » Sex Mai 24, 2019 19:35
por FilipeMSoares » Sex Mai 24, 2019 19:35
- 0 Respostas
- 5316 Exibições
- Última mensagem por FilipeMSoares

Sex Mai 24, 2019 19:35
Trigonometria
-
- cálculo de função
 por gutorocher » Dom Jul 25, 2010 19:40
por gutorocher » Dom Jul 25, 2010 19:40
- 12 Respostas
- 6338 Exibições
- Última mensagem por gutorocher

Qui Ago 05, 2010 16:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



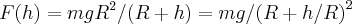
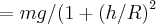 ...
...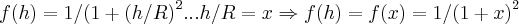 ...
...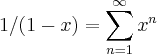 ,entao teremos
,entao teremos 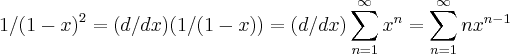 ...logo teremos:
...logo teremos: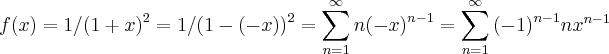 ...voltando a F(h),teremos...
...voltando a F(h),teremos...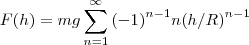 ...
...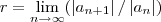 ...entao
...entao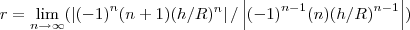








![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)