-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480024 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 537974 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501754 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 722908 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2156700 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Larissa28 » Seg Ago 17, 2015 23:21
por Larissa28 » Seg Ago 17, 2015 23:21
Calcule:
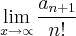
Sendo:
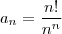
-
Larissa28
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Mar 21, 2015 17:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Produção
- Andamento: cursando
 por nakagumahissao » Seg Ago 17, 2015 23:57
por nakagumahissao » Seg Ago 17, 2015 23:57
Resolução:
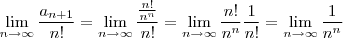
Vamos calcular alguns valores desta sequência:
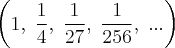
Como percebemos, os valores desta sequência convergem rapidamente para zero.
Assim:
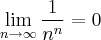

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por adauto martins » Qua Ago 19, 2015 11:06
por adauto martins » Qua Ago 19, 2015 11:06
pegando um gancho com o colega naka,podemos ter tbem:
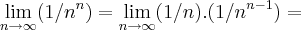
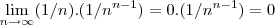
ou ainda...

...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo 2] Sequências
por Larissa28 » Qua Ago 12, 2015 00:20
- 4 Respostas
- 4961 Exibições
- Última mensagem por Larissa28

Seg Ago 17, 2015 23:06
Sequências
-
- [Cálculo] Convergência de Sequências
por Renato_RJ » Qua Ago 31, 2011 12:47
- 5 Respostas
- 2758 Exibições
- Última mensagem por Renato_RJ

Sáb Set 03, 2011 03:53
Cálculo: Limites, Derivadas e Integrais
-
- [Sequencias] Calculo do limite da sequencia
por Larissa28 » Qua Ago 05, 2015 01:09
- 2 Respostas
- 3762 Exibições
- Última mensagem por gshickluvx

Ter Nov 03, 2015 01:54
Sequências
-
- [Sequencias] Calculo do limite da sequencia
 por Larissa28 » Ter Ago 04, 2015 00:44
por Larissa28 » Ter Ago 04, 2015 00:44
- 4 Respostas
- 4094 Exibições
- Última mensagem por Larissa28

Qua Ago 05, 2015 20:45
Sequências
-
- [Sequencias] Sequencias Divergentes
por RafaelPereira » Sáb Jun 08, 2013 23:34
- 2 Respostas
- 3505 Exibições
- Última mensagem por RafaelPereira

Dom Jun 09, 2013 17:53
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
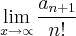
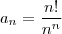

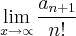
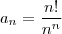

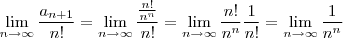
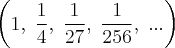
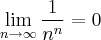


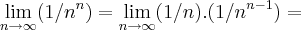
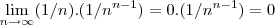 ou ainda...
ou ainda... ...
...
