[Série de Taylor] 4 primeiros termos

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Série de Taylor] 4 primeiros termos

Regras do fórum
Responder

[Série de Taylor] 4 primeiros termos

Mensagempor Crist » Sáb Mar 09, 2013 17:52

Alguém me socorre? Preciso a achar os quatro primeiros termos na série de Taylor para (x-1)e^x próximo de x = 1.
derivando a funçao: encontrei todas as derivadas iguais: todas iguais a zero, não sei o que faço :oops:
Crist
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 45
Registrado em: Qua Out 24, 2012 16:47
Formação Escolar: GRADUAÇÃO
Área/Curso: Matemática
Andamento: cursando
Voltar ao topo

Re: [Série de Taylor] 4 primeiros termos

Mensagempor young_jedi » Dom Mar 10, 2013 22:36

seja

f(x)=(x-1)e^x

então

f'(x)=e^x+(x-1)e^x

f''(x)=e^x+e^x+(x-1)e^x

f'''(x)=e^x+e^x+e^x+(x-1)e^x

f''''(x)=e^x+e^x+e^x+e^x+(x-1)e^x

então

f'(1)=e

f''(1)=2e

f'''(1)=3e

f''''(1)=4e
young_jedi
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1239
Registrado em: Dom Set 09, 2012 10:48
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica - UEL
Andamento: formado
Voltar ao topo

Re: [Série de Taylor] 4 primeiros termos

Mensagempor Crist » Dom Mar 10, 2013 23:12

:-D
Crist
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 45
Registrado em: Qua Out 24, 2012 16:47
Formação Escolar: GRADUAÇÃO
Área/Curso: Matemática
Andamento: cursando
Voltar ao topo
Responder

Voltar para Sequências

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: dúvida em uma questão em regra de 3!
Autor: leandro moraes - Qui Jul 01, 2010 12:41

pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.

78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?

Assunto: dúvida em uma questão em regra de 3!
Autor: Douglasm - Qui Jul 01, 2010 13:16

Observe o raciocínio:

10 pessoas - 9 dias - 135 toneladas

1 pessoa - 9 dias - 13,5 toneladas

1 pessoa - 1 dia - 1,5 toneladas

40 pessoas - 1 dia - 60 toneladas

40 pessoas - 30 dias - 1800 toneladas

Assunto: dúvida em uma questão em regra de 3!
Autor: leandro moraes - Qui Jul 01, 2010 13:18

pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.

Assunto: dúvida em uma questão em regra de 3!
Autor: leandro moraes - Qui Jul 01, 2010 13:21

leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.

valeu meu camarada.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

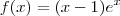
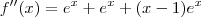
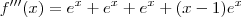
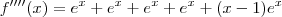
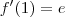
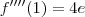
Índice do fórum