[SÉRIE] Teste da comparação

[luiz1903]

Boa tarde a todos, sou novo no fórum e gostaria de tirar umas dúvidas. A questão pede para vc dizer se a série converge ou diverge usando o teste da comparação. Teve tres questões que eu não consegui fazer:


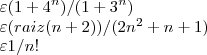
Sempre o somatório de n=1 até infinito.

Obrigado

[e8group]

Boa noite . O que você tentou , quais as dúvidas ?

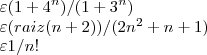
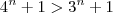A primeira pode compara com a série de termos constantes iguais a 1 (pois , , para todo n) .

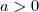Na terceira , para qualquer fixado , sempre 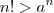para suficientemente grande .
Basta fixar qualquer e comparar a série 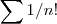com a geométrica \sum (1/a)^n [/tex] .

[luiz1903]

Obrigado por responder.

Na primeira eu peguei a série (6/5)^n, q é uma serie divergente e tem sempre bn<an (an é a série estudada). Sendo assim, an é divergente. Isso está correto?

Não entendi pq vc disse q n!>2^n. Eu preciso de uma série onde bn>an. Supondo a série 1/2^n, os primeiros termos dessa série serão 1/2, 1/4, 1/8... enquanto que os primeiros termos da série 1/n! serão 1/1, 1/2, 1/6 de forma que bn<an

[e8group]

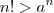Observe que se , isto automaticamente implica 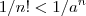(em geral para n suficientemente grande , entretanto , para caso particulares , como por exemplo .Neste caso basta impor que ) .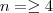

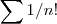Compleme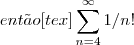ntando , se a série converge também converge .