 por ant_dii » Qua Jun 29, 2011 20:40
por ant_dii » Qua Jun 29, 2011 20:40
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvidas dois numeros irracionais
por hevhoram » Qui Jun 24, 2010 11:56
- 2 Respostas
- 2488 Exibições
- Última mensagem por MarceloFantini

Qui Jun 24, 2010 14:03
Álgebra Elementar
-
- Razão entre dois números
por lucas7 » Qui Fev 24, 2011 21:21
- 1 Respostas
- 2092 Exibições
- Última mensagem por lucas7

Sex Fev 25, 2011 08:44
Sistemas de Equações
-
- Maior entre dois numeros
por TiagoRodrigues » Qui Mar 01, 2012 14:37
- 5 Respostas
- 3949 Exibições
- Última mensagem por TiagoRodrigues

Sex Mar 02, 2012 11:18
Sistemas de Equações
-
- Demonstração de igualdade de dois números ao quadrado
por johnlaw » Sáb Mar 05, 2011 18:15
- 9 Respostas
- 5415 Exibições
- Última mensagem por johnlaw

Sex Mar 11, 2011 01:43
Álgebra Elementar
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17114 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é definida recursivamente pela equação
é definida recursivamente pela equação  para
para  , onde
, onde 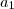 e
e 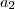 podem ser quaisquer numeros reais. Encontre
podem ser quaisquer numeros reais. Encontre  em termos de
em termos de 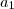 e
e 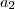 .
. e
e 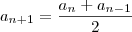 , pode-se fazer o seguinte:
, pode-se fazer o seguinte: .
.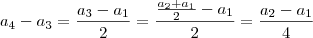



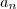 pedido.
pedido.

