 por CarolMarques » Sáb Out 20, 2012 22:08
por CarolMarques » Sáb Out 20, 2012 22:08
Não consigo calcular o limite abaixo:
lim
![\lim_{x->0}\frac{ \sqrt[]{x+2} + \sqrt[]{x+6} - \sqrt[]{6} - \sqrt[]{2}}{x} \lim_{x->0}\frac{ \sqrt[]{x+2} + \sqrt[]{x+6} - \sqrt[]{6} - \sqrt[]{2}}{x}](/latexrender/pictures/e380867ec7ffdb4d29991731818129fe.png)
Tentei multiplicar pelo conjugada mas não consigo chegar a lugar algum.Por favor me ajudem.
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por e8group » Sáb Out 20, 2012 23:38
por e8group » Sáb Out 20, 2012 23:38
Conhece L'hospital (L'Hôpital ) ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por CarolMarques » Dom Out 21, 2012 09:14
por CarolMarques » Dom Out 21, 2012 09:14
Eu queria resolver esse limite sem usar a regra de L'hospital
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por young_jedi » Dom Out 21, 2012 11:25
por young_jedi » Dom Out 21, 2012 11:25
separe os termos
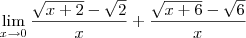
pode ser separados como soma dos limites
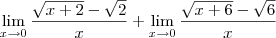
vamos resolver o primeiro limite
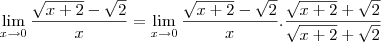
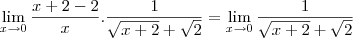
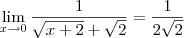
resolva o segundo limite e encontre o limite final
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por e8group » Dom Out 21, 2012 12:19
por e8group » Dom Out 21, 2012 12:19
Uma outra forma é fazer
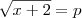
.Donde ,
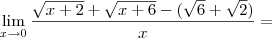
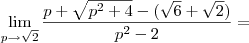
![\lim_{p\to \sqrt{2}} \left(\frac{p -\sqrt{2}}{(p-\sqrt{2})(p+\sqrt{2})} + \left[\frac{( \sqrt{p^2 +4}-\sqrt{6})(\sqrt{p^2 +4}+\sqrt{6})}{(p^2 -2)(\sqrt{p^2 +4}+\sqrt{6})}\right ] \right ) = \lim_{p\to \sqrt{2}} \left(\frac{p -\sqrt{2}}{(p-\sqrt{2})(p+\sqrt{2})} + \left[\frac{( \sqrt{p^2 +4}-\sqrt{6})(\sqrt{p^2 +4}+\sqrt{6})}{(p^2 -2)(\sqrt{p^2 +4}+\sqrt{6})}\right ] \right ) =](/latexrender/pictures/ba98c7f46f4a614985cd2c908bffd0f5.png)
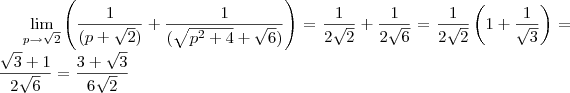
.
Portanto ,
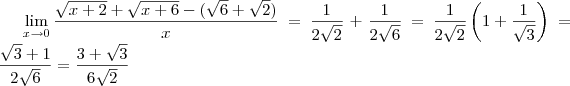
young_jedi , mesmo havendo uma indeterminação ,pode separar os limites por soma ? Não tem uma lei que diz que pode separar os limites se e somente os limites existem ? Fiquei em dúvida agora .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Dom Out 21, 2012 12:48
por MarceloFantini » Dom Out 21, 2012 12:48
Ele apenas reagrupou os termos e aplicou propriedades de limite.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Dúvida limite com raizes
por rqaugusto » Dom Abr 30, 2017 23:23
- 0 Respostas
- 3119 Exibições
- Última mensagem por rqaugusto

Dom Abr 30, 2017 23:23
Cálculo: Limites, Derivadas e Integrais
-
- Limite - Duvida
por Claudin » Qua Mai 18, 2011 18:32
- 3 Respostas
- 2603 Exibições
- Última mensagem por Claudin

Qua Mai 18, 2011 20:45
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Qua Mai 18, 2011 21:19
- 6 Respostas
- 3317 Exibições
- Última mensagem por Claudin

Qui Mai 19, 2011 12:31
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Qui Mai 19, 2011 09:20
- 5 Respostas
- 3081 Exibições
- Última mensagem por Claudin

Dom Mai 22, 2011 16:19
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Sáb Mai 21, 2011 16:17
- 18 Respostas
- 10932 Exibições
- Última mensagem por Claudin

Qui Mai 26, 2011 15:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x->0}\frac{ \sqrt[]{x+2} + \sqrt[]{x+6} - \sqrt[]{6} - \sqrt[]{2}}{x} \lim_{x->0}\frac{ \sqrt[]{x+2} + \sqrt[]{x+6} - \sqrt[]{6} - \sqrt[]{2}}{x}](/latexrender/pictures/e380867ec7ffdb4d29991731818129fe.png)

![\lim_{x->0}\frac{ \sqrt[]{x+2} + \sqrt[]{x+6} - \sqrt[]{6} - \sqrt[]{2}}{x} \lim_{x->0}\frac{ \sqrt[]{x+2} + \sqrt[]{x+6} - \sqrt[]{6} - \sqrt[]{2}}{x}](/latexrender/pictures/e380867ec7ffdb4d29991731818129fe.png)



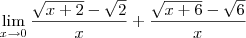
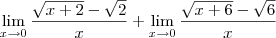
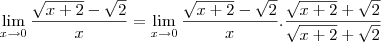
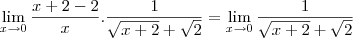
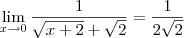

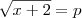 .Donde ,
.Donde , 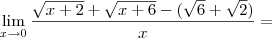
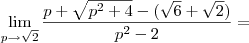
![\lim_{p\to \sqrt{2}} \left(\frac{p -\sqrt{2}}{(p-\sqrt{2})(p+\sqrt{2})} + \left[\frac{( \sqrt{p^2 +4}-\sqrt{6})(\sqrt{p^2 +4}+\sqrt{6})}{(p^2 -2)(\sqrt{p^2 +4}+\sqrt{6})}\right ] \right ) = \lim_{p\to \sqrt{2}} \left(\frac{p -\sqrt{2}}{(p-\sqrt{2})(p+\sqrt{2})} + \left[\frac{( \sqrt{p^2 +4}-\sqrt{6})(\sqrt{p^2 +4}+\sqrt{6})}{(p^2 -2)(\sqrt{p^2 +4}+\sqrt{6})}\right ] \right ) =](/latexrender/pictures/ba98c7f46f4a614985cd2c908bffd0f5.png)
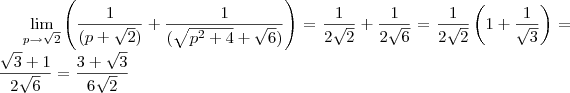 .
. 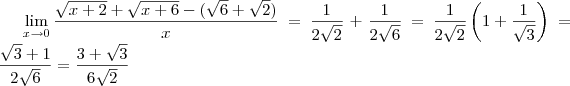





 , avisa que eu resolvo.
, avisa que eu resolvo.

