 por Cleyson007 » Ter Set 25, 2012 16:17
por Cleyson007 » Ter Set 25, 2012 16:17
Ache uma equação da reta tangente à curva y = 2x² + 3 que é paralela à reta 8x - y + 3 = 0.Bom, sei que a equação da reta tangente à curva é obtida por:
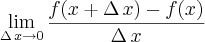
Resolvendo, encontro: f ' = 4x.
Para que a reta tangente seja paralela terá que ter o mesmo coeficiente angular. Correto?
Como prosseguir?
No aguardo.
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por young_jedi » Ter Set 25, 2012 16:30
por young_jedi » Ter Set 25, 2012 16:30
reescrenvo a equação da reta
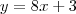
sendo assimo coeficiente angular é igual a 8
então
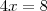
encontrando x voce encontra o ponto em que a reta paralela é tangente a cruva dai para encontrar o resto da equação é so substituição.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Ter Set 25, 2012 21:21
por Russman » Ter Set 25, 2012 21:21
Uma reta tangente a curva
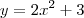
no ponto
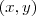
tem incinação

.
Se você procura uma reta tangente a curva

que seja paralela a reta

então esta deve ter inclinação igual a

, pois esta é a inclinação dessa reta.
Assim,
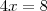
e , portanto,

.
Logo a reta tangente a curva

é da forma
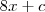
tal que
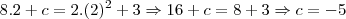
A reta procurada é
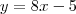
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equação reta tangente
por ezidia51 » Dom Ago 26, 2018 17:03
- 3 Respostas
- 4902 Exibições
- Última mensagem por Gebe

Dom Ago 26, 2018 19:52
Funções
-
- Equação da Reta Tangente
por Saturnino Nataniel » Ter Nov 06, 2012 21:42
- 1 Respostas
- 2022 Exibições
- Última mensagem por e8group

Qua Nov 14, 2012 10:27
Cálculo: Limites, Derivadas e Integrais
-
- [Equação da reta tangente]
por carolzinhag3 » Seg Out 03, 2016 19:43
- 1 Respostas
- 3451 Exibições
- Última mensagem por adauto martins

Sex Jan 06, 2017 15:18
Cálculo: Limites, Derivadas e Integrais
-
- [Equação da reta Tangente] derivadas
por lucasdemirand » Qua Ago 07, 2013 00:28
- 1 Respostas
- 2109 Exibições
- Última mensagem por young_jedi

Qua Ago 07, 2013 20:12
Cálculo: Limites, Derivadas e Integrais
-
- Achar a Equação de uma reta tangente
por Gabriela Amaral » Dom Set 10, 2017 13:41
- 1 Respostas
- 3168 Exibições
- Última mensagem por Gabriela Amaral

Dom Set 10, 2017 18:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
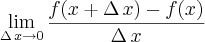

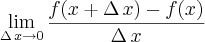

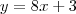
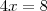

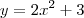 no ponto
no ponto 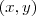 tem incinação
tem incinação  .
. que seja paralela a reta
que seja paralela a reta  então esta deve ter inclinação igual a
então esta deve ter inclinação igual a  , pois esta é a inclinação dessa reta.
, pois esta é a inclinação dessa reta.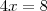 e , portanto,
e , portanto,  .
.  é da forma
é da forma 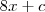 tal que
tal que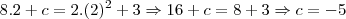
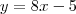 .
.