 por ivoski » Ter Ago 14, 2012 18:12
por ivoski » Ter Ago 14, 2012 18:12
Quando por uma integral dupla se calculou o volume do solido sob a surficie z = f(x,y), e acima da regiao D do plano xy, obteve-se a seguinte soma de integrais repetidas:
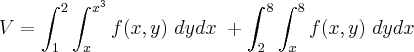
a) Esboce a regiao D e exprima V por uma integral repetida na ordem de intergração invertida.
b) Calcule V para f(x,y) =
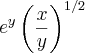
-
ivoski
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 14, 2012 17:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por LuizAquino » Qui Ago 23, 2012 18:32
por LuizAquino » Qui Ago 23, 2012 18:32
ivoski escreveu:Quando por uma integral dupla se calculou o volume do solido sob a surficie z = f(x,y), e acima da regiao D do plano xy, obteve-se a seguinte soma de integrais repetidas:
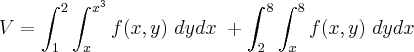
a) Esboce a regiao D e exprima V por uma integral repetida na ordem de intergração invertida.
b) Calcule V para f(x,y) =
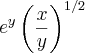
Vejamos o item a). A figura abaixo ilustra a região D.
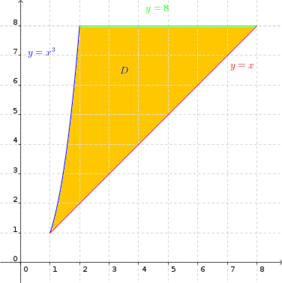
- figura.png (36.07 KiB) Exibido 2423 vezes
Veja que todo o trabalho se resumiu a determinar a região delimitada pelos gráficos de
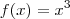
,
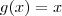
e
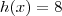
.
Analisando agora na ordem de integração invertida, precisamos escrever D no formato:
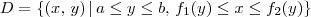
Analisando a figura acima, note que
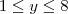
. Além disso, note que x está delimitado a esquerda pelo gráfico de
![f_1(y) = \sqrt[3]{y} f_1(y) = \sqrt[3]{y}](/latexrender/pictures/a64e5d19aa0389807b8b34d8c4571570.png)
. Por outro lado, x está delimitado a direita pelo gráfico de

. Desse modo, temos que:
![D = \{(x,\,y)\,|\,1\leq y \leq 8 ,\, \sqrt[3]{y}\leq x \leq y\} D = \{(x,\,y)\,|\,1\leq y \leq 8 ,\, \sqrt[3]{y}\leq x \leq y\}](/latexrender/pictures/8d8c8cc738f98ae99a389e792fb86283.png)
Podemos então escrever que:
![V = \int_1^8\int_{\sqrt[3]{y}}^{y} f(x,\,y)\,dx\,dy V = \int_1^8\int_{\sqrt[3]{y}}^{y} f(x,\,y)\,dx\,dy](/latexrender/pictures/308a2e1307fd584f4a02f656b76fc877.png)
Agora tente resolver o item b).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral dupla
por DanielFerreira » Sex Mar 16, 2012 23:56
- 2 Respostas
- 2867 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 17, 2012 19:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 2
por DanielFerreira » Dom Mar 18, 2012 12:44
- 5 Respostas
- 4149 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 22:34
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 4
 por DanielFerreira » Sex Abr 06, 2012 19:49
por DanielFerreira » Sex Abr 06, 2012 19:49
- 4 Respostas
- 3127 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 21:05
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 5
por DanielFerreira » Sex Abr 06, 2012 20:00
- 2 Respostas
- 1912 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 20:16
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 6
 por DanielFerreira » Sáb Abr 14, 2012 22:54
por DanielFerreira » Sáb Abr 14, 2012 22:54
- 1 Respostas
- 1625 Exibições
- Última mensagem por LuizAquino

Dom Abr 15, 2012 23:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
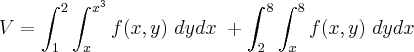
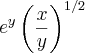

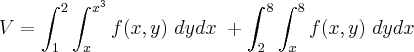
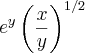

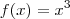 ,
, 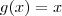 e
e 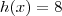 .
.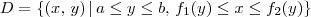
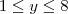 . Além disso, note que x está delimitado a esquerda pelo gráfico de
. Além disso, note que x está delimitado a esquerda pelo gráfico de ![f_1(y) = \sqrt[3]{y} f_1(y) = \sqrt[3]{y}](/latexrender/pictures/a64e5d19aa0389807b8b34d8c4571570.png) . Por outro lado, x está delimitado a direita pelo gráfico de
. Por outro lado, x está delimitado a direita pelo gráfico de  . Desse modo, temos que:
. Desse modo, temos que:![D = \{(x,\,y)\,|\,1\leq y \leq 8 ,\, \sqrt[3]{y}\leq x \leq y\} D = \{(x,\,y)\,|\,1\leq y \leq 8 ,\, \sqrt[3]{y}\leq x \leq y\}](/latexrender/pictures/8d8c8cc738f98ae99a389e792fb86283.png)
![V = \int_1^8\int_{\sqrt[3]{y}}^{y} f(x,\,y)\,dx\,dy V = \int_1^8\int_{\sqrt[3]{y}}^{y} f(x,\,y)\,dx\,dy](/latexrender/pictures/308a2e1307fd584f4a02f656b76fc877.png)
