Um oleoduto tem a forma da curva
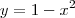 com
com 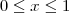 , x e y medidos em quilômetros. Será construída uma cerca tangente à curva
, x e y medidos em quilômetros. Será construída uma cerca tangente à curva 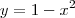 no ponto P diferente (0,1) . Determine as coordenadas do ponto P de modo que a área da região triangular formada pela cerca e pelos eixos seja mínima.
no ponto P diferente (0,1) . Determine as coordenadas do ponto P de modo que a área da região triangular formada pela cerca e pelos eixos seja mínima.Eu pensei assim:
A área triangular é formada pela tangente a curva de y no primeiro quadrante com x entre 0 e 1.
A reta tangente é a hipotenusa do triangulo que quero minimizar a área.
Encontrando a equação da reta tangente:

reta tangente: (x= a é o ponto da curva
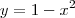 onde a reta tangente minimiza o triângulo)
onde a reta tangente minimiza o triângulo)
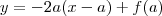
sei também que a hipotenusa que é a reta tangente vale
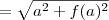
Tentei sair disso várias vezes mas faço um monte de contas e nunca chego em lugar algum.
Se alguém puder me ajudar, agradeço



 a reta tangente de
a reta tangente de 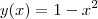 no ponto
no ponto 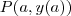 . Como você ja calculou, teremos
. Como você ja calculou, teremos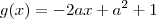 .
. que satisfazem o problema. Ambos com mesma ordenada e de abscissas simétricas. É fácil verificar este fato desenhando um ponto
que satisfazem o problema. Ambos com mesma ordenada e de abscissas simétricas. É fácil verificar este fato desenhando um ponto 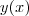 entre
entre  e
e  e , em seguida, entre
e , em seguida, entre  e
e 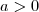 a inclinação da mesma deve ser negativa, como previsto pela equação de
a inclinação da mesma deve ser negativa, como previsto pela equação de 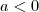 a inclinação deve ser positiva como também previsto.
a inclinação deve ser positiva como também previsto. e
e  é dada por
é dada por 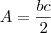 . Assim, como queremos determinar o ponto
. Assim, como queremos determinar o ponto  , é pertinente que expressemos
, é pertinente que expressemos 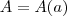 , isto é, a área do triângulo como uma função de
, isto é, a área do triângulo como uma função de 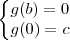 ,
, 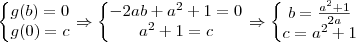 .
.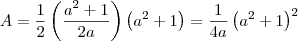 .
.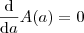 .
.
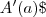 e igualando a 0
e igualando a 0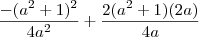
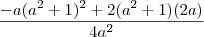
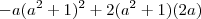 = 0 , a diferente de zero
= 0 , a diferente de zero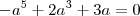
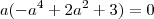 , a não pode ser zero
, a não pode ser zero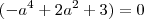

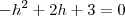
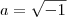 e
e 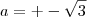
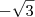 , -2) ou (
, -2) ou ( , -2)
, -2)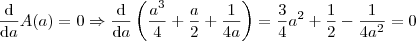
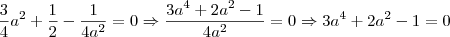
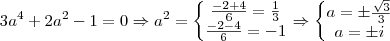
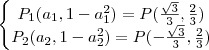
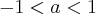 .
.




