-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478020 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530604 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 494192 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 702300 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2115285 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por DanielFerreira » Dom Jun 03, 2012 16:14
por DanielFerreira » Dom Jun 03, 2012 16:14
danjr5 escreveu:Calcule
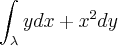
onde

é uma curva, cuja imagem é o segmento de extremidades (1, 1) e (2, 2), orientada de (1, 1) para (2, 2).
Fiz assim:



Como o campo vetorial não é conservativo, não posso aplicar o Teorema

.
Então, pelo Teorema de Green:
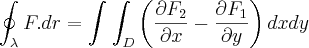
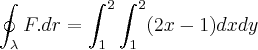
![\oint_{\lambda}^{}F.dr = \int_{1}^{2}\left[x^2 - x \right]_{1}^{2}dy \oint_{\lambda}^{}F.dr = \int_{1}^{2}\left[x^2 - x \right]_{1}^{2}dy](/latexrender/pictures/7d23524dfed7b2f04148f4b80df61dc0.png)
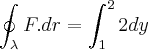
![\oint_{\lambda}^{}F.dr = \left[2y \right]_{1}^{2} \oint_{\lambda}^{}F.dr = \left[2y \right]_{1}^{2}](/latexrender/pictures/73fcbbf2243246a0f7578398992d7c22.png)

Mas, de acordo com o gabarito a resposta certa é
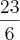
.
Desde já agradeço.
Att,
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Russman » Dom Jun 03, 2012 18:48
por Russman » Dom Jun 03, 2012 18:48
Eu acredito que sua solução está correta.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por DanielFerreira » Dom Jun 03, 2012 19:14
por DanielFerreira » Dom Jun 03, 2012 19:14
Russman,
valeu pela atenção!
O Teorema de Green aplica-se quando o caminho é fechado, então não pode ser aplicado em

.
Numa conversa com o professor de Cálculo, ele deixou bem claro que deveríamos 'priorizar' os Teoremas(Green, Campo Gradiente) na resolução de Integrais de Linha. Enfim, entendi que a Definição deveria ser a última opção.
Pela Definição:
Parametrizando

:



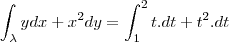
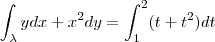
![\int_{\lambda }ydx + x^2dy = \left [\frac{t^2}{2} + \frac{t^3}{3} \right ]_{1}^{2} \int_{\lambda }ydx + x^2dy = \left [\frac{t^2}{2} + \frac{t^3}{3} \right ]_{1}^{2}](/latexrender/pictures/c6fafb63e059a81f58db7f1b9f9b1a11.png)
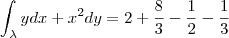
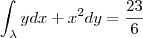
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral de linha
por calc3 » Dom Jun 07, 2015 11:43
- 0 Respostas
- 2779 Exibições
- Última mensagem por calc3

Dom Jun 07, 2015 11:43
Cálculo: Limites, Derivadas e Integrais
-
- Integral de linha - Trabalho
 por Bruhh » Ter Jul 05, 2011 16:55
por Bruhh » Ter Jul 05, 2011 16:55
- 1 Respostas
- 2821 Exibições
- Última mensagem por LuizAquino

Ter Jul 05, 2011 19:10
Cálculo: Limites, Derivadas e Integrais
-
- [Integral de Linha] Teoria
por Claudin » Qui Jul 25, 2013 23:47
- 0 Respostas
- 1675 Exibições
- Última mensagem por Claudin

Qui Jul 25, 2013 23:47
Cálculo: Limites, Derivadas e Integrais
-
- [Integral de linha] problema
 por Ahoush123 » Sáb Nov 28, 2015 15:20
por Ahoush123 » Sáb Nov 28, 2015 15:20
- 0 Respostas
- 2480 Exibições
- Última mensagem por Ahoush123

Sáb Nov 28, 2015 15:20
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Integral de linha
por pedro22132938 » Sex Dez 30, 2016 01:28
- 3 Respostas
- 6047 Exibições
- Última mensagem por adauto martins

Seg Jan 02, 2017 15:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 61 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
onde
é uma curva, cuja imagem é o segmento de extremidades (1, 1) e (2, 2), orientada de (1, 1) para (2, 2).



 .
.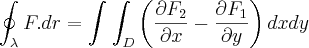
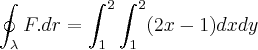
![\oint_{\lambda}^{}F.dr = \int_{1}^{2}\left[x^2 - x \right]_{1}^{2}dy \oint_{\lambda}^{}F.dr = \int_{1}^{2}\left[x^2 - x \right]_{1}^{2}dy](/latexrender/pictures/7d23524dfed7b2f04148f4b80df61dc0.png)
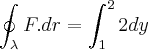
![\oint_{\lambda}^{}F.dr = \left[2y \right]_{1}^{2} \oint_{\lambda}^{}F.dr = \left[2y \right]_{1}^{2}](/latexrender/pictures/73fcbbf2243246a0f7578398992d7c22.png)

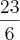 .
.





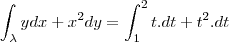
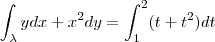
![\int_{\lambda }ydx + x^2dy = \left [\frac{t^2}{2} + \frac{t^3}{3} \right ]_{1}^{2} \int_{\lambda }ydx + x^2dy = \left [\frac{t^2}{2} + \frac{t^3}{3} \right ]_{1}^{2}](/latexrender/pictures/c6fafb63e059a81f58db7f1b9f9b1a11.png)
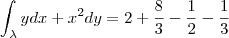
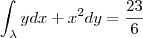
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)