-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477676 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528352 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 491908 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 695867 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2103967 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por edu2012 » Ter Mai 29, 2012 16:38
por edu2012 » Ter Mai 29, 2012 16:38
Boa tarde, gostaria de um exemplo de integral imprópria quando ela converge ou Diverge até agora não estou entendendo.
um exemplo
?
? x+1/(x²+2x) dx
1
desde de já agradeço.
-
edu2012
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 29, 2012 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica
- Andamento: cursando
 por LuizAquino » Ter Mai 29, 2012 20:53
por LuizAquino » Ter Mai 29, 2012 20:53
edu2012 escreveu:Boa tarde, gostaria de um exemplo de integral imprópria quando ela converge ou Diverge até agora não estou entendendo.
um exemplo
?
? x+1/(x²+2x) dx
1
Do jeito que você escreveu, a integral seria:
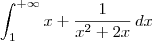
Mas ao que parece, a integral original seria:

Se esse for o caso, então você deveria ter escrito algo como:
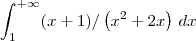
Note a importância do uso adequado dos parênteses.
Supondo que essa seja a integral que você deseja calcular, a primeira coisa que você precisa fazer é resolver a integral indefinida. Nesse caso, você irá obter:
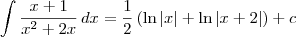
Depois que você resolveu a integral indefinida, você pode partir para resolver a integral imprópria. Você deve seguir o seguinte procedimento:
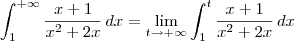
![= \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t = \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t](/latexrender/pictures/5254ecef9540c8883a9438aca418ea60.png)
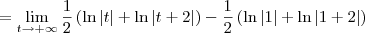
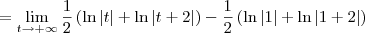
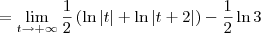
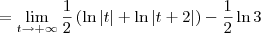
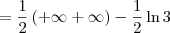

Como o resultado da integral imprópria foi infinito, temos que ela é divergente.
Se no final dos cálculos você tivesse encontrado como resultado um valor fixo, então a integral imprópria seria convergente. Por exemplo, considere a seguinte integral imprópria:
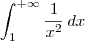
Note que:

Sendo assim, temos que:
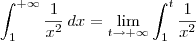
![= \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t = \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t](/latexrender/pictures/765779293a3854676a11157002910beb.png)

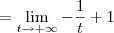
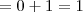
Como o resultado da integral imprópria foi um valor fixo, temos que ela é convergente. Nesse caso, diremos que essa integral imprópria converge para 1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por edu2012 » Qua Mai 30, 2012 09:24
por edu2012 » Qua Mai 30, 2012 09:24
Luis Aquino Obrigado.
-
edu2012
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 29, 2012 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 4070 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- Calculo 2 AJUDA
por rodrigojuara » Seg Jun 15, 2015 23:38
- 0 Respostas
- 4532 Exibições
- Última mensagem por rodrigojuara

Seg Jun 15, 2015 23:38
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Ajuda
por leandrofsm » Qui Jan 05, 2017 14:59
- 1 Respostas
- 7261 Exibições
- Última mensagem por Cleyson007

Ter Jan 10, 2017 17:56
Cálculo
-
- Ajuda com Calculo (?)
 por opb1212 » Qui Ago 31, 2017 20:32
por opb1212 » Qui Ago 31, 2017 20:32
- 0 Respostas
- 1025 Exibições
- Última mensagem por opb1212

Qui Ago 31, 2017 20:32
Cálculo: Limites, Derivadas e Integrais
-
- exercício calculo do VAL Ajuda
por nhrd » Qui Dez 11, 2008 23:20
- 0 Respostas
- 1870 Exibições
- Última mensagem por nhrd

Qui Dez 11, 2008 23:20
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 32 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



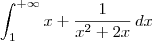

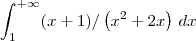
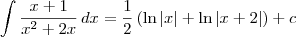
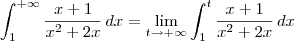
![= \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t = \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t](/latexrender/pictures/5254ecef9540c8883a9438aca418ea60.png)
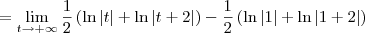
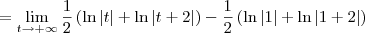
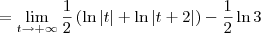
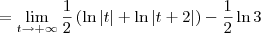
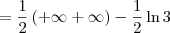

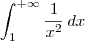

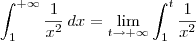
![= \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t = \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t](/latexrender/pictures/765779293a3854676a11157002910beb.png)

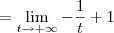
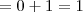




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.