Fabio Wanderley escreveu:"Ao calcular a integral
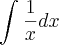
, Joãozinho procedeu da seguinte maneira.
Fazendo
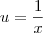
, e

, podemos tomar v = x, e teremos
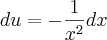
.
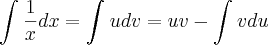
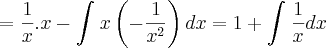
Sendo
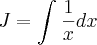
, temos então J = 1 + J, logo 0 = 1.
Onde está o erro no argumento de Joãozinho?"
Fabio Wanderley escreveu:Segue um exercício que não consigo revolvê-lo...
Alguém pode me ajudar?
O erro está no fato que Joãozinho esqueceu das constantes que aparecem no desenvolver da integração por partes.
Quando estamos resolvendo integração por partes, aparecem duas constantes durante o processo, que no final são "resumidas" em uma só.
Vejamos um exemplo. Suponha que você deseja calcular:
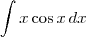
Fazendo u = x e
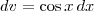
, temos que du = dx e
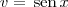
. Temos então que:
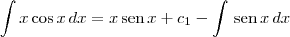
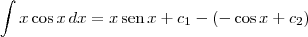
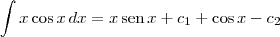
Como

e

são constantes, podemos chamar

de uma outra constante. Digamos que vamos chamar de c. Ficamos então com:
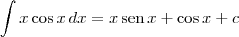
Com a prática, acabamos "ignorando" essas constantes em cada passo do desenvolvimento, sendo que apenas colocamos uma constante no final das contas. Mas é justamente esse fato de ignorar as constantes que fez Joãozinho errar. Ele deveria ter escrito algo como:
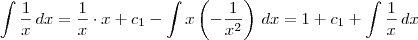
Se ele tivesse agora definido que
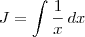
, ele poderia escrever que

. Nesse contexto, ele iria concluir que

. Se ele tivesse agora substituído essa constante no desenvolvimento da integral, ele teria chegado a uma conclusão óbvia: J = J.
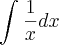 , Joãozinho procedeu da seguinte maneira.
, Joãozinho procedeu da seguinte maneira.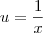 , e
, e  , podemos tomar v = x, e teremos
, podemos tomar v = x, e teremos 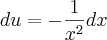 .
.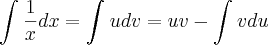
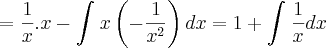
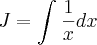 , temos então J = 1 + J, logo 0 = 1.
, temos então J = 1 + J, logo 0 = 1.

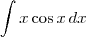
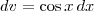 , temos que du = dx e
, temos que du = dx e 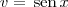 . Temos então que:
. Temos então que: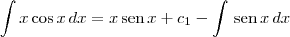
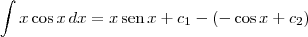
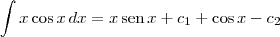
 e
e  são constantes, podemos chamar
são constantes, podemos chamar  de uma outra constante. Digamos que vamos chamar de c. Ficamos então com:
de uma outra constante. Digamos que vamos chamar de c. Ficamos então com: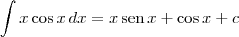
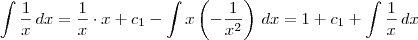
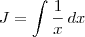 , ele poderia escrever que
, ele poderia escrever que  . Nesse contexto, ele iria concluir que
. Nesse contexto, ele iria concluir que  . Se ele tivesse agora substituído essa constante no desenvolvimento da integral, ele teria chegado a uma conclusão óbvia: J = J.
. Se ele tivesse agora substituído essa constante no desenvolvimento da integral, ele teria chegado a uma conclusão óbvia: J = J.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.