por Grasi » Qui Jun 25, 2009 00:22
por Grasi » Qui Jun 25, 2009 00:22
Uma partícula se move sobre uma reta e tem equação horária s = 5t^2 – 8t + 2. Qual é a posição da partícula para t = 0? A partícula, em t = 0, se move para a direita ou para a esquerda? Qual é o instante em que a partícula reverte o sentido de seu movimento? Em que instante a partícula volta a ocupar a mesma posição que tinha em t = 0? Qual é a velocidade da partícula em cada instante t?
Já tentei encontrar a solução em 3 livros q tenho, mas os exemplos e teorias não estão me ajudando.
Peço a gentileza para ajudar-me, agradeço desde já. Muito obrigada!
-
Grasi
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jun 24, 2009 23:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por wyncler » Sex Jul 03, 2009 23:22
por wyncler » Sex Jul 03, 2009 23:22
Bem pelo q eu entedi se vc derivar a primeira vc vai ter a posição da particula, dae vc pode fazer as substituições possiveis para encontrar o que e pedido.
Espero ter ajudado.
-
wyncler
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jul 03, 2009 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologica
- Andamento: cursando
 por Marcampucio » Sáb Jul 04, 2009 22:11
por Marcampucio » Sáb Jul 04, 2009 22:11
Grasi escreveu:Uma partícula se move sobre uma reta e tem equação horária s = 5t^2 – 8t + 2. Qual é a posição da partícula para t = 0? A partícula, em t = 0, se move para a direita ou para a esquerda? Qual é o instante em que a partícula reverte o sentido de seu movimento? Em que instante a partícula volta a ocupar a mesma posição que tinha em t = 0? Qual é a velocidade da partícula em cada instante t?
Já tentei encontrar a solução em 3 livros q tenho, mas os exemplos e teorias não estão me ajudando.
Peço a gentileza para ajudar-me, agradeço desde já. Muito obrigada!
a) posição em t=0
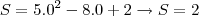
b) o que se pode dizer em t=0 é que a partícula se move em sentido da origem da trajetória em movimento retrógrado e retardado. Sua velocidade é
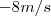
e a aceleração é
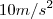
c) reversão do sentido e velocidade a cada instante
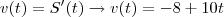
a reversão ocorre no instante em que

, portanto
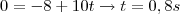
d) instante em que volta a ocupar mesma posição que em t=0
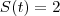
nos remete a
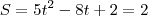
ou
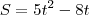
que nos dá as soluções

ou
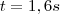
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1997 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:12
- 1 Respostas
- 3303 Exibições
- Última mensagem por Molina

Qui Jun 25, 2009 11:05
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:15
- 1 Respostas
- 2552 Exibições
- Última mensagem por Molina

Qui Jun 25, 2009 11:30
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:16
- 1 Respostas
- 2084 Exibições
- Última mensagem por Neperiano

Sáb Set 17, 2011 15:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:18
- 0 Respostas
- 1441 Exibições
- Última mensagem por Grasi

Qui Jun 25, 2009 00:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


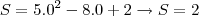
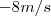 e a aceleração é
e a aceleração é 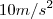
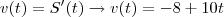 a reversão ocorre no instante em que
a reversão ocorre no instante em que  , portanto
, portanto 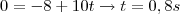
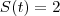 nos remete a
nos remete a 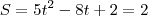 ou
ou 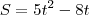 que nos dá as soluções
que nos dá as soluções  ou
ou