 por rycherr » Ter Mai 08, 2012 01:32
por rycherr » Ter Mai 08, 2012 01:32
quero saber como se faz a integral de sec(x)dx utilizando o metodo de funções racionais de seno e cosseno.
aquele método no qual se substitui Z=tg(x/2) cos(x)=(1-z²)/(1+z²) e sen(x)=2Z/1+Z²
Obrigado.
-
rycherr
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 08, 2012 01:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ggbb
- Andamento: cursando
 por LuizAquino » Ter Mai 08, 2012 12:04
por LuizAquino » Ter Mai 08, 2012 12:04
rycherr escreveu:quero saber como se faz a integral de sec(x) dx utilizando o metodo de funções racionais de seno e cosseno.
aquele método no qual se substitui Z=tg(x/2) cos(x)=(1-z²)/(1+z²) e sen(x)=2Z/1+Z²
Note que:
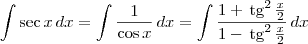
Agora faça a substituição:

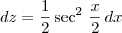
Lembrando da identidade trigonométrica
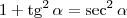
, podemos reescrever
dz como sendo:
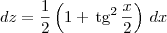
Agora tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rycherr » Ter Mai 08, 2012 16:28
por rycherr » Ter Mai 08, 2012 16:28
sim, até ai eu fiz, parei em ln l 1+cosx+senx/1+cosx-senx l
se igualar isso á ln l secx+tgx l prova-se que é verdadeiro, mas como chegar em ln l secx+tgx l sómente desdobrando a formula?
-
rycherr
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 08, 2012 01:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ggbb
- Andamento: cursando
 por LuizAquino » Ter Mai 08, 2012 17:01
por LuizAquino » Ter Mai 08, 2012 17:01
rycherr escreveu:sim, até ai eu fiz, parei em ln l 1+cosx+senx/1+cosx-senx l
se igualar isso á ln l secx+tgx l prova-se que é verdadeiro, mas como chegar em ln l secx+tgx l sómente desdobrando a formula?
Se você já tinha desenvolvido até certa parte, então por que não enviou o seu desenvolvimento?
Note que isso economizaria o tempo da pessoa que está lhe ajudando, pois ela poderia apenas corrigir as partes que estavam erradas. Ou ainda, apenas informar como prosseguir.
Além disso, informar sobre suas tentativas faz parte das
Regras deste Fórum. Vide a Regra 1.
De qualquer modo, refaça as suas contas, pois você deveria chegar em:
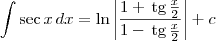
A partir daí, temos que:
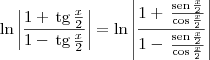
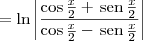
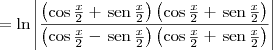
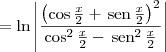
Agora tente continuar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problemas usando derivadas
 por ezidia51 » Sex Set 07, 2018 17:21
por ezidia51 » Sex Set 07, 2018 17:21
- 60 Respostas
- 120602 Exibições
- Última mensagem por ezidia51

Sáb Dez 29, 2018 22:21
Cálculo: Limites, Derivadas e Integrais
-
- Problema usando a lógica
por virginia » Sáb Abr 27, 2013 11:52
- 1 Respostas
- 1570 Exibições
- Última mensagem por Jhennyfer

Sáb Abr 27, 2013 17:22
Lógica
-
- Usando o teorema angular de tales
 por Roni Martins » Sáb Fev 13, 2010 15:30
por Roni Martins » Sáb Fev 13, 2010 15:30
- 2 Respostas
- 3727 Exibições
- Última mensagem por Roni Martins

Dom Fev 14, 2010 11:53
Geometria Plana
-
- Encontrar Dominio usando logaritimo
por barizom » Sáb Mar 27, 2010 13:58
- 2 Respostas
- 1941 Exibições
- Última mensagem por barizom

Sáb Mar 27, 2010 20:48
Funções
-
- Encontrar velocidade usando a Integral
por renanrdaros » Dom Abr 17, 2011 04:03
- 8 Respostas
- 4953 Exibições
- Última mensagem por renanrdaros

Seg Abr 18, 2011 11:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



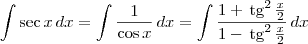

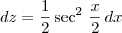
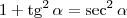 , podemos reescrever dz como sendo:
, podemos reescrever dz como sendo: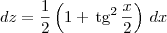


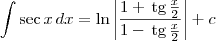
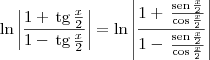
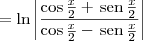
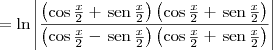
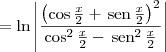


 .
.



