 por dileivas » Ter Mai 01, 2012 09:54
por dileivas » Ter Mai 01, 2012 09:54
Oi galera, estou resolvendo uma EDO e caí na seguinte derivada:
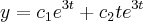
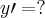
Alguém poderia me explicar com um passo-a-passo, plz?
Sei que vai ficar algo assim
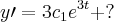
O problema é justamente a segunda derivada...
Obrigado =)
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por dileivas » Ter Mai 01, 2012 17:18
por dileivas » Ter Mai 01, 2012 17:18
Entendi! Obrigado =)
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Calcular a derivada em relação a x
por Brunorp » Qua Mar 16, 2016 14:35
- 0 Respostas
- 1712 Exibições
- Última mensagem por Brunorp

Qua Mar 16, 2016 14:35
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Duvida em derivada da definição.
por paulohenrique_ » Dom Dez 09, 2012 16:05
- 1 Respostas
- 1931 Exibições
- Última mensagem por young_jedi

Dom Dez 09, 2012 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Calcular Derivada ln(secx+tgx)
por shantziu » Seg Set 05, 2011 16:55
- 3 Respostas
- 4219 Exibições
- Última mensagem por shantziu

Qua Set 07, 2011 17:01
Cálculo: Limites, Derivadas e Integrais
-
- Como Calcular derivada
por Amanda j » Qui Jun 06, 2013 22:00
- 1 Respostas
- 1743 Exibições
- Última mensagem por Arthur_Bulcao

Seg Jun 10, 2013 04:02
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo calcular essa derivada!!!
por Catalao » Qua Mai 09, 2012 19:51
- 3 Respostas
- 2375 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 14:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
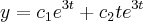
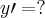
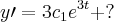

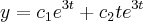
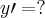
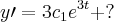

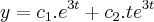
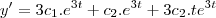
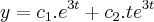

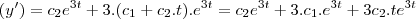


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.