-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477937 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530004 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493583 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 700544 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2112161 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por jmoura » Sáb Mar 31, 2012 23:58
por jmoura » Sáb Mar 31, 2012 23:58
Me deparei com uma questão de uma prova antiga que não estou conseguindo resolver:
" Verifique se existe um número real L tal que a função f definida por
f(x)=
![cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right)](/latexrender/pictures/892305de84ef21387bf3e2e208782b9c.png)
, se x>0 e
f(x)= L, se x=0
é contínua no intervalo [0, +

). "
-
jmoura
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mar 23, 2012 22:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por NMiguel » Dom Abr 01, 2012 08:06
por NMiguel » Dom Abr 01, 2012 08:06

é continua em
![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png)
se e só se
![\[f(0)=\lim_{x \to 0}f(x)\] \[f(0)=\lim_{x \to 0}f(x)\]](/latexrender/pictures/72e6d29fe38d7ce2a5f838ddb5bf29ef.png)
, ou seja,
![\[L=\lim_{x \to 0}f(x)\] \[L=\lim_{x \to 0}f(x)\]](/latexrender/pictures/ddc8ec56eed64e87853d096eb414dc95.png)
.
Como
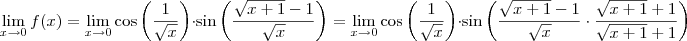
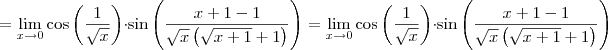
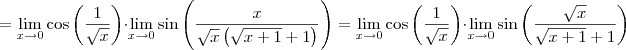
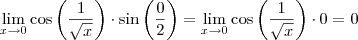
Assim,

é continua em
![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png)
se e só se

Editado pela última vez por
NMiguel em Dom Abr 01, 2012 19:14, em um total de 1 vez.
-
NMiguel
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Ter Abr 19, 2011 17:09
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
-
 por NMiguel » Dom Abr 01, 2012 19:13
por NMiguel » Dom Abr 01, 2012 19:13
Sim. De facto é necessário. Sem isso, não poderíamos afirmar que este limite é igual a

. Obrigado pela observação.
Fica então um complemento à resolução.
Sabemos que
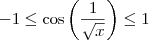
.
Assim,
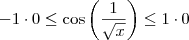
, ou seja,
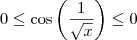
.
Daqui, sai que

.
Assim, fica completa a demonstração

-
NMiguel
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Ter Abr 19, 2011 17:09
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como resolver essa questao
por Thassya » Qui Mai 21, 2009 23:25
- 1 Respostas
- 3825 Exibições
- Última mensagem por marciommuniz

Sex Mai 22, 2009 12:23
Trigonometria
-
- Como resolver essa questão da Ufpel?
 por ativirginis » Seg Fev 27, 2012 15:02
por ativirginis » Seg Fev 27, 2012 15:02
- 1 Respostas
- 4442 Exibições
- Última mensagem por LuizAquino

Ter Fev 28, 2012 18:41
Funções
-
- Sem ideia de como resolver essa questão.
por jemourafer » Sáb Abr 28, 2012 00:38
- 1 Respostas
- 1366 Exibições
- Última mensagem por Russman

Sáb Abr 28, 2012 04:52
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver essa questão de probabilidade
por amanda s » Sex Nov 15, 2013 15:11
- 1 Respostas
- 2412 Exibições
- Última mensagem por DanielFerreira

Sex Nov 29, 2013 00:33
Probabilidade
-
- Como resolver essa equação?
por viniciusantonio » Qua Out 21, 2009 19:17
- 1 Respostas
- 3657 Exibições
- Última mensagem por carlos r m oliveira

Qui Out 22, 2009 14:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 39 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right)](/latexrender/pictures/892305de84ef21387bf3e2e208782b9c.png) , se x>0 e
, se x>0 e  ). "
). "
![cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right). sen\left(\frac{\sqrt[]{x+1}-1}{\sqrt[]{x}} \right)](/latexrender/pictures/892305de84ef21387bf3e2e208782b9c.png) , se x>0 e
, se x>0 e  ). "
). "
 é continua em
é continua em ![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png) se e só se
se e só se ![\[f(0)=\lim_{x \to 0}f(x)\] \[f(0)=\lim_{x \to 0}f(x)\]](/latexrender/pictures/72e6d29fe38d7ce2a5f838ddb5bf29ef.png) , ou seja,
, ou seja, ![\[L=\lim_{x \to 0}f(x)\] \[L=\lim_{x \to 0}f(x)\]](/latexrender/pictures/ddc8ec56eed64e87853d096eb414dc95.png) .
.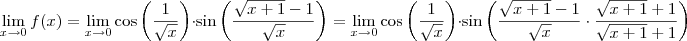
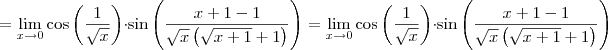
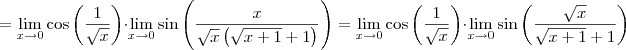
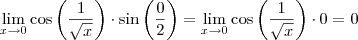
 é continua em
é continua em ![\[[0,+\infty )\] \[[0,+\infty )\]](/latexrender/pictures/b697848248ebb3044e04902ad94130ca.png) se e só se
se e só se 

![cos\left(\frac{1}{\sqrt[]{x}} \right) cos\left(\frac{1}{\sqrt[]{x}} \right)](/latexrender/pictures/0bd3dfe730b93b200c4c64156d0c0c8b.png) é limitada, e aplicar o Teorema do Confronto para provar que o limite é igual a zero?
é limitada, e aplicar o Teorema do Confronto para provar que o limite é igual a zero?
 . Obrigado pela observação.
. Obrigado pela observação.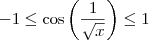 .
.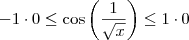 , ou seja,
, ou seja, 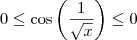 .
. .
.






