Gabriel_DvT escreveu:Usando a definição, provar que:

Gabriel_DvT escreveu:A resolução é a seguinte:
Vamoso mostrar que, dado
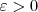
existe
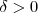
, tal que:

sempre que

Da desigualdade que envolve

temos:

 Necessitamos agora substituir |x+4| por um valor constante. Neste caso vamos supor
Necessitamos agora substituir |x+4| por um valor constante. Neste caso vamos supor  e então, de
e então, de  , seguem as seguintes desigualdades equivalentes:
, seguem as seguintes desigualdades equivalentes: <--- (Eis a duvida 1): Por que fazer isso? Simplesmente não sei de onde ele tirou isso.
Você deseja analisar o que acontece quando x está
próximo de 4. Nesse sentido, podemos nos concentrar
apenas no intervalo 4 - 1 < x < 4 + 1. Também poderíamos, se quiséssemos, nos concentrar
apenas no intervalo 4 - 1/2 < x < 4 + 1/2. Ou ainda, nos concentrar
apenas no intervalo 4 - 1/4 < x < 4 + 1/4. Em resumo, escolhendo qualquer número

tal que

, podemos nos concentrar
apenas no intervalo

.
Em particular, por simplicidade, vamos
escolher nos concentrar no intervalo 4 - 1 < x < 4 + 1. Lembrando que pela definição de limites o x não precisa ser
igual a 4, essa inequação é equivalente a

. Ou seja, olhando para definição de limite, nós estamos escolhendo

.
Vamos agora somar 4 a ambas as partes da desigualdade 4 - 1 < x < 4 + 1. Desse modo, temos que 7 < x + 4 < 9. Note que o número x + 4 está no intervalo (7, 9). Isso significa que esse número é positivo e portanto podemos escrever que x + 4 = |x + 4| nesse intervalo. Desse modo, podemos dizer que |x + 4| < 9.
Fazendo então

, note que podemos afirmar que:

Lembrando da definição de limites, note que fazer

significa que
escolhemos 
.
Ora, lembre-se também que antes tínhamos escolhido

.
Finalmente, vamos usar qual desses dois valores de

? Nós vamos usar o
menor dos dois, isto é, vamos escolher

(aqui a notação

representa o menor dos dois valores a e b. Por exemplo,

).
Mas por que escolher o menor dos dois? Escolhendo

como o menor dos dois valores, vamos garantir que duas relações irão acontecer:
(i)

;
(ii)

.
Sendo assim, para essa escolha de

podemos dizer que:

Em resumo, provamos que dado um

existe um
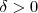
(que é definido como

) tal que:

Mas isso é exatamente a definição formal para:

Gabriel_DvT escreveu:Bom, estou começando a estudar cálculo para o curso de engenharia de computação e estou fazendo isso praticamente por conta própria.
Se você tiver interesse em assistir videoaulas sobre Cálculo, então eu gostaria de recomendar o meu canal no YouTube:
http://www.youtube.com/LCMAquinoEu espero que ele possa lhe ajudar em seus estudos.

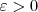 existe
existe 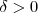 , tal que:
, tal que: sempre que
sempre que 
 temos:
temos:

 e então, de
e então, de  , seguem as seguintes desigualdades equivalentes: <--- (Eis a duvida 1): Por que fazer isso? Simplesmente não sei de onde ele tirou isso.
, seguem as seguintes desigualdades equivalentes: <--- (Eis a duvida 1): Por que fazer isso? Simplesmente não sei de onde ele tirou isso.




 , temos que, se
, temos que, se  , então <---- Também não compreendi esse
, então <---- Também não compreendi esse 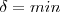




 tal que
tal que  , podemos nos concentrar
, podemos nos concentrar  .
. . Ou seja, olhando para definição de limite, nós estamos escolhendo
. Ou seja, olhando para definição de limite, nós estamos escolhendo  .
. , note que podemos afirmar que:
, note que podemos afirmar que:
 .
. (aqui a notação
(aqui a notação  representa o menor dos dois valores a e b. Por exemplo,
representa o menor dos dois valores a e b. Por exemplo,  ).
). ;
; .
.
 existe um
existe um 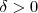 (que é definido como
(que é definido como 

