 por Fabio Wanderley » Sáb Mar 24, 2012 13:14
por Fabio Wanderley » Sáb Mar 24, 2012 13:14
Olá, pessoal
Tendo o limite
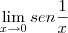
Como faço para verificar isso?
Usei o conceito de limites laterais e obtive que quando x tende a 0- terei

; quando x tende a 0+ terei
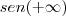
.
Como sen é uma função ímpar:
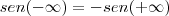
Disso, teríamos que os limites laterais são diferentes, portando não existe o limite dado. Mas isto está certo? Posso trabalhar com
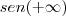
?
-
Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por MarceloFantini » Sáb Mar 24, 2012 14:49
por MarceloFantini » Sáb Mar 24, 2012 14:49
Este limite não existe. Porém, a única justificativa que me lembro agora é usando sequências. Não faz sentido escrever

ou mais infinito. Evite.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Verificar a Resolução
por eli83 » Ter Out 09, 2012 09:13
- 3 Respostas
- 1856 Exibições
- Última mensagem por eli83

Qua Out 10, 2012 00:39
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Verificar a Resolução I
por eli83 » Ter Out 09, 2012 09:55
- 3 Respostas
- 1735 Exibições
- Última mensagem por eli83

Qua Out 10, 2012 00:31
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Conceito de Existência
por eli83 » Qua Out 10, 2012 10:33
- 4 Respostas
- 2584 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Existência de limite e se existir, pertence aos reais ou com
por Douglas16 » Qui Fev 28, 2013 20:36
- 3 Respostas
- 2699 Exibições
- Última mensagem por Jhonata

Qui Fev 28, 2013 22:52
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
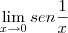
 ; quando x tende a 0+ terei
; quando x tende a 0+ terei 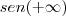 .
.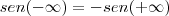
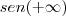 ?
?

 ou mais infinito. Evite.
ou mais infinito. Evite.
