-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478868 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536317 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 499981 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 718763 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2144416 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por kika_sanches » Sex Mar 23, 2012 14:42
por kika_sanches » Sex Mar 23, 2012 14:42
OLá!!
Alguém que possa me ajudar a resolver esse exercício por favor?!
Usando o método de substituição, resolva a integral:
|(x^2-4)^5 . x dx
Obrigada desde já!
-
kika_sanches
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Mar 22, 2012 18:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sex Mar 23, 2012 15:17
por MarceloFantini » Sex Mar 23, 2012 15:17
Faça a substituição
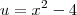
. Procure trabalhar disso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por kika_sanches » Sex Mar 23, 2012 15:28
por kika_sanches » Sex Mar 23, 2012 15:28
Essa é a parte que eu sei...
o du q não entendo!
Como acho e com que valores substituo?
Obrigada!
-
kika_sanches
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Mar 22, 2012 18:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sex Mar 23, 2012 15:33
por MarceloFantini » Sex Mar 23, 2012 15:33
O
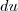
é a derivada de u. Você não substitui valores, você substituirá na função. Neste caso:
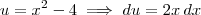
. Daí,
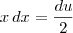
. Logo,
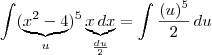
. Termine.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por kika_sanches » Sex Mar 23, 2012 15:35
por kika_sanches » Sex Mar 23, 2012 15:35
Obrigada meeeessmooo!!!
você não sabe como eu estou penando para aprender sozinha!!
A faculdade me disponibiliza os videos explicativos e só!
simplismente nos deixa sozinhos para aprender!!
Obrigada novamente!
-
kika_sanches
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Mar 22, 2012 18:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição / Integral por partes
por Carlos28 » Seg Out 19, 2015 12:25
- 1 Respostas
- 2708 Exibições
- Última mensagem por nakagumahissao

Seg Out 19, 2015 23:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição
por Aliocha Karamazov » Qui Fev 23, 2012 23:57
- 2 Respostas
- 1985 Exibições
- Última mensagem por MarceloFantini

Sex Fev 24, 2012 12:07
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Dom Nov 18, 2012 10:46
- 1 Respostas
- 1555 Exibições
- Última mensagem por young_jedi

Dom Nov 18, 2012 10:54
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Seg Nov 19, 2012 16:23
- 7 Respostas
- 3876 Exibições
- Última mensagem por MarceloFantini

Ter Nov 20, 2012 21:45
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição
por manuel_pato1 » Seg Dez 31, 2012 15:17
- 2 Respostas
- 1647 Exibições
- Última mensagem por manuel_pato1

Qui Jan 03, 2013 14:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 118 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





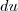 é a derivada de u. Você não substitui valores, você substituirá na função. Neste caso:
é a derivada de u. Você não substitui valores, você substituirá na função. Neste caso: 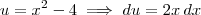 . Daí,
. Daí, 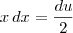 . Logo,
. Logo, 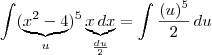 . Termine.
. Termine.




 , avisa que eu resolvo.
, avisa que eu resolvo.

