-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477873 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529531 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493080 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 699098 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2109596 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por joaofonseca » Qui Mar 22, 2012 14:57
por joaofonseca » Qui Mar 22, 2012 14:57
Seja,
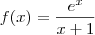
Para encontrar a derivada de f em x=0 faço,

que fica,
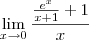
Ao substituir obtenho uma indeterminação do tipo, 0/0. Sei que a técnica de levantamento desta indeterminhação passa por fatorar de forma a encontrar o fator comum.Mas eu não estou a ver como fatorar o numerador.
Graficamente já verifiquei que a derivada existe em x=0.
Podem me dar alguma pista de como começar?
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qui Mar 22, 2012 17:55
por LuizAquino » Qui Mar 22, 2012 17:55
joaofonseca escreveu:Seja,
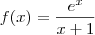
Para encontrar a derivada de f em x=0 faço,

que fica,
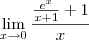
Na verdade, fica:
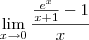
joaofonseca escreveu:Ao substituir obtenho uma indeterminação do tipo, 0/0.
Com a alteração que indiquei acima, de fato temos essa indeterminação.
joaofonseca escreveu:Sei que a técnica de levantamento desta indeterminação passa por fatorar de forma a encontrar o fator comum. Mas eu não estou a ver como fatorar o numerador.
Nesse caso a técnica não é por fatoração.
joaofonseca escreveu:Graficamente já verifiquei que a derivada existe em x=0.
Ok.
joaofonseca escreveu:Podem me dar alguma pista de como começar?
Note que o limite pode ser escrito como:
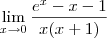
Agora faça a substituição
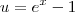
. Desse modo, quando
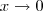
temos que
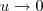
. Além disso, temos que
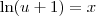
.
Temos então que:
![\lim_{x \to 0} \dfrac{e^x - x - 1}{x(x+1)} = \lim_{u \to 0} \dfrac{u - \ln(u + 1)}{[\ln(u + 1)][\ln(u + 1) + 1]} \lim_{x \to 0} \dfrac{e^x - x - 1}{x(x+1)} = \lim_{u \to 0} \dfrac{u - \ln(u + 1)}{[\ln(u + 1)][\ln(u + 1) + 1]}](/latexrender/pictures/6f4c12d29c0316448abcec2fefcc5097.png)
Agora tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por joaofonseca » Qui Mar 22, 2012 18:37
por joaofonseca » Qui Mar 22, 2012 18:37
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como resolver esta Formula
por ana maria » Ter Dez 17, 2013 11:57
- 6 Respostas
- 3463 Exibições
- Última mensagem por ana maria

Ter Dez 17, 2013 15:26
Matemática Financeira
-
- [Inequeções] Como resolver esta?
por alienante » Seg Dez 30, 2013 10:18
- 2 Respostas
- 1890 Exibições
- Última mensagem por Renato_RJ

Seg Dez 30, 2013 14:27
Álgebra Elementar
-
- Logarítmos - Como resolver esta expressão
por petras » Qui Out 20, 2016 10:35
- 3 Respostas
- 7031 Exibições
- Última mensagem por DanielFerreira

Seg Out 24, 2016 22:08
Logaritmos
-
- Como resolver esta questão da banca COMPERVE?
por matemarcos » Qui Jan 11, 2018 22:26
- 1 Respostas
- 4947 Exibições
- Última mensagem por DanielFerreira

Qui Jan 25, 2018 11:43
Sistemas de Equações
-
- Não consigo resolver esta questão.
por marianacarvalhops » Sex Mai 15, 2009 21:10
- 2 Respostas
- 2174 Exibições
- Última mensagem por admin

Sáb Mai 16, 2009 21:12
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 24 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
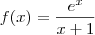

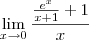


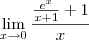
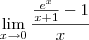
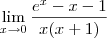
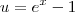 . Desse modo, quando
. Desse modo, quando 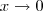 temos que
temos que 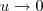 . Além disso, temos que
. Além disso, temos que 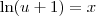 .
.![\lim_{x \to 0} \dfrac{e^x - x - 1}{x(x+1)} = \lim_{u \to 0} \dfrac{u - \ln(u + 1)}{[\ln(u + 1)][\ln(u + 1) + 1]} \lim_{x \to 0} \dfrac{e^x - x - 1}{x(x+1)} = \lim_{u \to 0} \dfrac{u - \ln(u + 1)}{[\ln(u + 1)][\ln(u + 1) + 1]}](/latexrender/pictures/6f4c12d29c0316448abcec2fefcc5097.png)

![\lim_{u\to 0} \frac{u-ln(u+1)}{ln(u+1)[ln(u+1)+1]} \lim_{u\to 0} \frac{u-ln(u+1)}{ln(u+1)[ln(u+1)+1]}](/latexrender/pictures/d3fec2154faf9d307fe061139865e2a8.png)
![\lim_{u\to 0} \frac{u}{ln(u+1)[ln(u+1)+1]}-\lim_{u\to 0}\frac{ln(u+1)}{ln(u+1)[ln(u+1)+1]} \lim_{u\to 0} \frac{u}{ln(u+1)[ln(u+1)+1]}-\lim_{u\to 0}\frac{ln(u+1)}{ln(u+1)[ln(u+1)+1]}](/latexrender/pictures/d4a100a8ddebdd57989dc8b5289963f0.png)

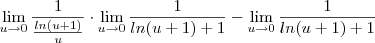
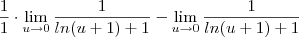

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.