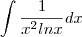
Tentando por partes, fiz
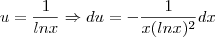 e
e 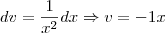
Fiz todos os passos da técnica de resolução por partes e cheguei a
 . Alguém pode me ajudar?
. Alguém pode me ajudar?
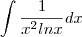
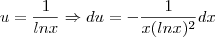 e
e 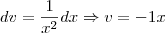
 . Alguém pode me ajudar?
. Alguém pode me ajudar?




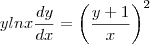




Aliocha Karamazov escreveu:Quando ela não pode ser escrita em funções elementares, não há nenhuma maneira de calculá-la?

Aliocha Karamazov escreveu:Se fosse uma integral definida, vinda de uma aplicação, seria possível fazer uma aproximação de seu resultado?


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante