por Leandro_Araujo » Seg Fev 27, 2012 01:01
por Leandro_Araujo » Seg Fev 27, 2012 01:01
Boa noite a todos.
Tenho uma grande dificuldade em operações algébricas. Não consigo encontrar a resposta do livro para a derivada da seguinte função:
f(x)=2x/(1+x)^3
Usando as regras de derivação cheguei até o seguinte ponto:
f'(x)=(1+x)^3*2x' - 2x*(1+x)^3'/((1+x)^3)^2
f'(x)=2*(1+x)^3 - 2x*3(x+1)^2/(1+3)^6
deste ponto em diante nada que eu tente me faz chegar no resultado:
f'(x)=2(1-2x)/(1+x)^4
Agradeço a atenção de todos!
-
Leandro_Araujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Fev 27, 2012 00:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Eletrônica e de Telecomunicações
- Andamento: cursando
 por MarceloFantini » Seg Fev 27, 2012 01:11
por MarceloFantini » Seg Fev 27, 2012 01:11
Leandro, poderia usar LaTeX no seu desenvolvimento para que possamos entender onde foi seu erro?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Leandro_Araujo » Seg Fev 27, 2012 01:57
por Leandro_Araujo » Seg Fev 27, 2012 01:57
Mais é claro! É meu primeiro post.
Então segue:
A função é a seguinte:
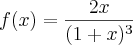
Consegui chegar até o seguinte ponto:
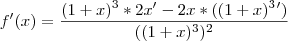
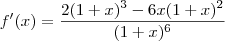
Não consigo achar o seguinte resultado:
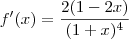
Tenho certeza que meu problema são as operações algébricas. Agradeço a atenção.
-
Leandro_Araujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Fev 27, 2012 00:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Eletrônica e de Telecomunicações
- Andamento: cursando
 por Leandro_Araujo » Seg Fev 27, 2012 02:31
por Leandro_Araujo » Seg Fev 27, 2012 02:31
Como sou persistente, acabei de achar o resultado.
De certa forma era simples, bastava colocar um fator em evidencia:
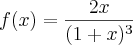
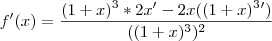
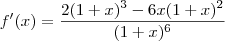
Colocando

em evidencia, temos:
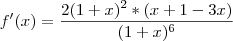
Simplificando
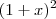
com
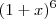
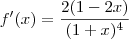
Bom de qualquer forma agradeço, e o fato de ver minha resolução no fórum me fez enxergar as funções de outra forma. Vou continuar meus estudos. Abçs.
-
Leandro_Araujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Fev 27, 2012 00:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Eletrônica e de Telecomunicações
- Andamento: cursando
 por LuizAquino » Seg Fev 27, 2012 11:52
por LuizAquino » Seg Fev 27, 2012 11:52
Leandro_Araujo escreveu:Tenho uma grande dificuldade em operações algébricas.
Leandro_Araujo escreveu:Tenho certeza que meu problema são as operações algébricas.
Leandro_Araujo escreveu:Como sou persistente, acabei de achar o resultado.
De certa forma era simples, bastava colocar um fator em evidencia:
Eu recomendo você assista a videoaula do Nerckie sobre fatoração. O título da videoaula é "Matemática Zero - Aula 11 - Fatoração". Ela está disponível no canal dele no YouTube:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Leandro_Araujo » Seg Fev 27, 2012 14:10
por Leandro_Araujo » Seg Fev 27, 2012 14:10
LuizAquino escreveu:Leandro_Araujo escreveu:Tenho uma grande dificuldade em operações algébricas.
Leandro_Araujo escreveu:Tenho certeza que meu problema são as operações algébricas.
Leandro_Araujo escreveu:Como sou persistente, acabei de achar o resultado.
De certa forma era simples, bastava colocar um fator em evidencia:
Eu recomendo você assista a videoaula do Nerckie sobre fatoração. O título da videoaula é "Matemática Zero - Aula 11 - Fatoração". Ela está disponível no canal dele no YouTube:
http://www.youtube.com/nerckie
Estou assistindo e gostando bastante. Já tinha visto outras videoaulas do Nerckie. Algebra é imprescindível para o cálculo. Vlw!
-
Leandro_Araujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Fev 27, 2012 00:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Eletrônica e de Telecomunicações
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [CALCULO] derivada de função composta
por beel » Ter Out 04, 2011 22:45
- 4 Respostas
- 2230 Exibições
- Última mensagem por beel

Dom Out 16, 2011 16:55
Cálculo: Limites, Derivadas e Integrais
-
- [CALCULO] derivada de função composta 2
por beel » Ter Out 04, 2011 22:58
- 5 Respostas
- 3119 Exibições
- Última mensagem por beel

Qui Out 13, 2011 12:33
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Calculando a derivada da função
por karenfreitas » Sáb Mai 28, 2016 11:03
- 1 Respostas
- 2966 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 22:08
Cálculo: Limites, Derivadas e Integrais
-
- dê a sua ajuda para o iniciante!
por leandro moraes » Qui Jan 28, 2010 11:17
- 4 Respostas
- 4209 Exibições
- Última mensagem por leandro moraes

Qui Jan 28, 2010 16:28
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




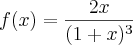
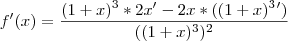
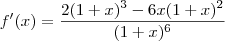
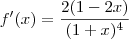
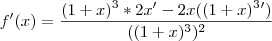
 em evidencia, temos:
em evidencia, temos: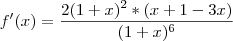
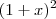 com
com