[Integral] Substituição
Pessoal, minha dúvida não é nem como resolver a integral, mas sim saber por que o método de substituição funciona. Para isso, vou usar um exemplo bem simples.
Quando eu quero calcular a integral indefinida
Uso a substituição, fazendo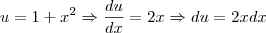
Aí vem:
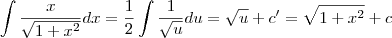
Quanto a isso, sem problemas. Mas, se a derivada de u em relação a x pode ser escrita como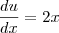 , é só uma questão de notação. Por que, ao "passar dx para o outro lado", a integral é calculada corretamente? Afinal, como
, é só uma questão de notação. Por que, ao "passar dx para o outro lado", a integral é calculada corretamente? Afinal, como 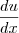 é uma notação, em tese, eu não poderia fazer isso. Não estou duvidando que funciona (porque dá certo!), mas quero saber o porquê. Obrigado.
é uma notação, em tese, eu não poderia fazer isso. Não estou duvidando que funciona (porque dá certo!), mas quero saber o porquê. Obrigado.
Quando eu quero calcular a integral indefinida

Uso a substituição, fazendo
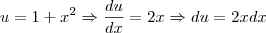
Aí vem:
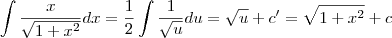
Quanto a isso, sem problemas. Mas, se a derivada de u em relação a x pode ser escrita como
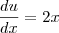 , é só uma questão de notação. Por que, ao "passar dx para o outro lado", a integral é calculada corretamente? Afinal, como
, é só uma questão de notação. Por que, ao "passar dx para o outro lado", a integral é calculada corretamente? Afinal, como 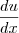 é uma notação, em tese, eu não poderia fazer isso. Não estou duvidando que funciona (porque dá certo!), mas quero saber o porquê. Obrigado.
é uma notação, em tese, eu não poderia fazer isso. Não estou duvidando que funciona (porque dá certo!), mas quero saber o porquê. Obrigado.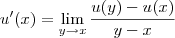
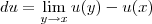
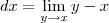
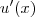 e
e 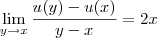
 , temos que:
, temos que: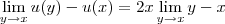
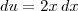
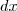 como uma forma diferencial, dando um sentido então a isto.
como uma forma diferencial, dando um sentido então a isto.