Resolva o problema de valor inicial.
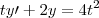
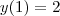
Eu comeceu divindo tudo por t:
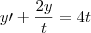
Agora, preciso encontrar o fator integrante, que é a função
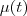 . Como está no livro, é preciso multiplica a equação por
. Como está no livro, é preciso multiplica a equação por 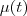 , o que dá:
, o que dá: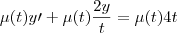
Agora, eu preciso encontrar uma função
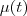 tal que
tal que ![[\mu(t)y]\prime=\mu(t)y\prime+\mu\prime(t)y=\mu(t)y\prime +\mu(t)\frac{2y}{t} [\mu(t)y]\prime=\mu(t)y\prime+\mu\prime(t)y=\mu(t)y\prime +\mu(t)\frac{2y}{t}](/latexrender/pictures/7ee7670e09a461204863f0d1cec6a0f9.png)
Bem, isso se resume a encontrar
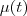 tal que
tal que 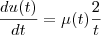 . Eu fiz dessa maneira:
. Eu fiz dessa maneira: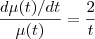
Como
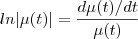 , temos que
, temos que 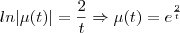
No entanto, no livro, está que
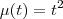
Alguém poderia me ajudar, dizendo onde e por que errei? Agradeço desde já.


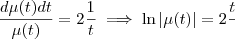 . Você deve colocar
. Você deve colocar 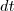 do outro lado e integrar os dois lados da equação, não apenas um. Veja:
do outro lado e integrar os dois lados da equação, não apenas um. Veja: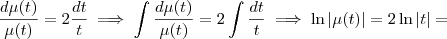
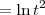 .
. 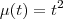 . Acredito que esteja faltando uma constante também.
. Acredito que esteja faltando uma constante também.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.