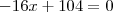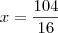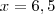Olá
plugpc!
Este é um problema de otimização.
Mas, no primeiro passo, não pense em
derivada.
Siga os passos da construção como deve ter feito para concluir sobre a expressão do volume.
Embora, não utilizaremos o volume: concentre-se na área.
Se você obteve a expressão do volume é porque já conseguiu identificar as medidas das arestas e montar a figura, isso é bom.
Note que o problema cita
área lateral. Não confunda com área total da superfície.
Como você já possui as medidas das arestas, escreva
a expressão da
área lateral.
Repare que a
área lateral também é uma função de

.
Agora, para entender a resolução deste problema e outros semelhantes de otimização, pergunte-se:
Qual o "tipo" desta função? Qual a sua "família"? Consigo esboçar o gráfico dela?
É importante que você reflita sobre estas perguntas e encontre respostas!
Você deverá obter que a
área lateral é representada por:
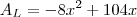
Pois bem: você verá que a
função área lateral está representada por uma expressão de segundo grau, cujo gráfico é de uma parábola!
Também podemos escrevê-la assim:
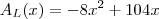
Ou ainda:
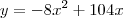
O segundo passo é refazer a pergunta do problema, olhando para o gráfico!
Pergunte-se: quando esta área é máxima? Para qual valor de

?
A pergunta é bem pertinente, uma vez que a parábola é côncava para baixo e possui um valor máximo!
O terceiro passo é, somente agora, se preocupar com o conceito de
derivada.
Pensar em
derivada como o
coeficiente angular da reta tangente à curva!
Acredite, você precisa "enxergar" as infinitas retas tangentes, "navegando", tangenciando a curva: a parábola!
Ao mesmo tempo em que pensa no coeficiente angular, o ângulo de inclinação de cada reta tangente!
Pois bem, pergunto:
Qual a inclinação da reta tangente no ponto máximo da parábola?
Resposta: ela é paralela ao eixo

, portanto, inclinação zero.
Novamente, conceito de
derivada:
derivada é o coeficiente angular da reta tangente no ponto!
É daqui que concluímos então que: quando a
derivada da
função área lateral for nula, teremos o ponto máximo procurado.
Após entendidas estas etapas, o término do problema é simples.
Calculamos a
derivada:

E apenas escrevemos a pergunta: quando a
derivada é nula?
Qual o valor de

quando
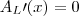
?
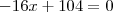

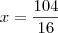
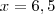
Espero ter ajudado no entendimento.
Bons estudos!


 .
.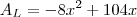
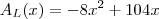
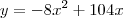

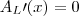 ?
?