![\sqrt[]{c^2 -x^2} \sqrt[]{c^2 -x^2}](/latexrender/pictures/b3304603faeb048033782759cc868708.png) , o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.
, o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.Eu fiz assim,
![\int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx \int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx](/latexrender/pictures/b64c4dda60d5d659594a1d6d46224715.png)
ficou:
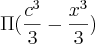 , aplicados de -c até c
, aplicados de -c até cfiquei muito em duvida em como fazer dai em diante

![\sqrt[]{c^2 -x^2} \sqrt[]{c^2 -x^2}](/latexrender/pictures/b3304603faeb048033782759cc868708.png) , o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.
, o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.![\int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx \int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx](/latexrender/pictures/b64c4dda60d5d659594a1d6d46224715.png)
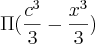 , aplicados de -c até c
, aplicados de -c até c
beel escreveu:Considere a regiao delimitada pelo grafico da função[/tex], o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.
Eu fiz assim,
ficou:, aplicados de -c até c
fiquei muito em duvida em como fazer dai em diante
integrate pi*(sqrt(c^2 - x^2))^2 dx
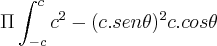 , mas nao to conseguindo achar uma primitiva...fuuui naquele site mas nao achei nenhuma resultado
, mas nao to conseguindo achar uma primitiva...fuuui naquele site mas nao achei nenhuma resultado
beel escreveu:a integral é definida... o enunciado fala que a função é delimitada pelas retas x=c e x=-c...fiz uma substituição trigonometrica e cai nisso, mas nao to conseguindo achar uma primitiva...fuuui naquele site mas nao achei nenhuma resultado
 . Ou seja, você poderá verificar o passo a passo de como obter a primitiva de
. Ou seja, você poderá verificar o passo a passo de como obter a primitiva de 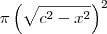 .
.![x\in [-c,\, c] x\in [-c,\, c]](/latexrender/pictures/a6b7fb11bcf6827a85be0b88a4ad3c85.png) temos que
temos que 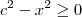 , o que significa que podemos escrever:
, o que significa que podemos escrever: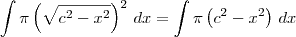
Indefinite integrals:
![\int_{-c}^{c} \pi\left(\sqrt{c^2 - x^2}\right)^2 dx = \left[\pi c^2 x - \frac{\pi x^3}{3}\right]_{-c}^c \int_{-c}^{c} \pi\left(\sqrt{c^2 - x^2}\right)^2 dx = \left[\pi c^2 x - \frac{\pi x^3}{3}\right]_{-c}^c](/latexrender/pictures/fc257704505b88926deaa1af9daf4109.png)
![=\left[\pi c^2 \cdot c - \frac{\pi \cdot c^3}{3}\right] - \left[\pi c^2\cdot (-c) - \frac{\pi \cdot (-c)^3}{3}\right] =\left[\pi c^2 \cdot c - \frac{\pi \cdot c^3}{3}\right] - \left[\pi c^2\cdot (-c) - \frac{\pi \cdot (-c)^3}{3}\right]](/latexrender/pictures/fca794af4cc81e93c4b7db5f12d0e0ba.png)
![=\left[\pi c^3 - \frac{\pi c^3}{3}\right] - \left[-\pi c^3 + \frac{\pi c^3}{3}\right] =\left[\pi c^3 - \frac{\pi c^3}{3}\right] - \left[-\pi c^3 + \frac{\pi c^3}{3}\right]](/latexrender/pictures/6c1ecf3069941da497ceca7596ae1af6.png)

integrate pi*(sqrt(c^2 - x^2))^2 dx x=-c..c
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes