Ana_Rodrigues escreveu:Eu já procurei vídeos no youtube explicando, inclusive vídeos de autores que são moderadores deste fórum, e lá tinha o exemplo da função modular f(x)=|x|, que não era diferenciável, porém era contínua isto porque a função possuía um bico em x=0.
Você deve estar se referindo ao Exemplo 3 da vídeo-aula "10. Cálculo I - Função Derivada" disponível em meu
canal no YouTube.
Vejamos o enunciado desse exemplo.
Exemplo 3: A função f(x)=|x| é diferenciável em 0?Como foi explicado nessa mesma vídeo aula, uma função é diferenciável no ponto x=c se o limite abaixo existe e é finito:

O exemplo em questão quer avaliar se a função é diferenciável em x=0. Ou seja, precisamos analisar se o limite abaixo existe e é finito:
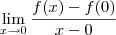
Ora, mas esse limite é mesmo que:

Aplicando a definição de módulo, obtemos que:


Já que esses limites laterais são distintos, temos que não existe

.
Já que esse limite não existe, temos que a função não é diferenciável em x=0.
Vale destacar que essa função é diferenciável em qualquer outro ponto x=c, com c não nulo. Faça o teste!
Ana_Rodrigues escreveu:Neste caso a função é contínua em x=0?por que?
Sim.
Lembre-se que por definição, uma função f é contínua em x=c se ocorrer:

Sendo assim, para saber se a função é contínua em x=0 será necessário verificar se ocorre:

Note que nesse caso isso ocorre:

Por outro lado, f(0)=|0|=0. Sendo assim, temos que:

Podemos então afirmar que f é contínua em x=0.
Vale destacar que essa função é contínua em qualquer outro ponto x=c, com c não nulo. Faça o teste!





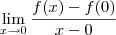








 , avisa que eu resolvo.
, avisa que eu resolvo.

