antonelli2006 escreveu:Em que pontos a reta tangente à curva
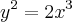
é perpendicular à reta
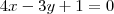
?
Derivando implicitamente a curva dada, temos que:
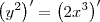
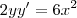
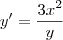
Sabemos então que
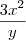
é o coeficiente angular da reta tangente a curva no ponto (x, y).
Já que 4/3 é o coeficiente angular da reta
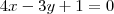
, para que ela seja perpendicular a reta tangente a curva, deve ocorrer:
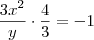

Falta agora determinar os pontos (x, y) sobre a curva
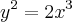
tais que

. Isto é, basta resolver o sistema:
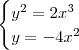
Resolvendo esse sistema obtemos
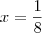
e
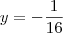
(aqui desconsideramos a solução x=0 e y=0).
Portanto, apenas no ponto

a reta tangente a curva
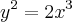
é perpendicular a reta
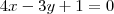
.
Observaçãoantonelli2006 escreveu:Fiz a derivada de
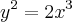
, igualando

, e deu
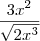
.
Aqui você esqueceu que:
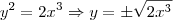
Portanto, temos que:
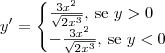
Note que não há derivada em y=0. Fica mais fácil perceber isso fazendo uma ilustração do gráfico dessa curva.
Para continuar a resolução a partir daqui, você teria que analisar dois casos:
(i)
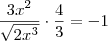
;
(ii)
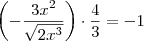
;
Note que (i) não tem solução real, enquanto que (ii) tem solução x = 1/8 (e portanto y = -1/16).
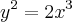 é perpendicular à reta
é perpendicular à reta 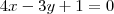 ?
?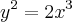 , igualando
, igualando ![y=\sqrt[]{2x^3} y=\sqrt[]{2x^3}](/latexrender/pictures/a3aa8f99dcd42bfd67325d9308013166.png) , e deu
, e deu ![\frac{3x^2}{\sqrt[]{2x^3}} \frac{3x^2}{\sqrt[]{2x^3}}](/latexrender/pictures/423832f23318f8fde4f2d298c8e5dae9.png) .
. .
. :
:![\frac{3x^2}{\sqrt[]{2x^3}}.\frac{4}{3}=-1 \frac{3x^2}{\sqrt[]{2x^3}}.\frac{4}{3}=-1](/latexrender/pictures/2d4e39b603c9897290e7a2e6446e753e.png)
![\frac{4x^2}{\sqrt[]{2x^3}}=-1 \frac{4x^2}{\sqrt[]{2x^3}}=-1](/latexrender/pictures/dabd8c77b38cc4611869e86e738bf482.png)



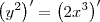

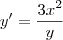
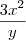 é o coeficiente angular da reta tangente a curva no ponto (x, y).
é o coeficiente angular da reta tangente a curva no ponto (x, y).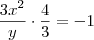

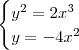
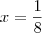 e
e 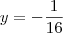 (aqui desconsideramos a solução x=0 e y=0).
(aqui desconsideramos a solução x=0 e y=0). a reta tangente a curva
a reta tangente a curva  , e deu
, e deu 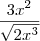 .
.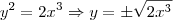
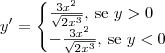
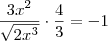 ;
;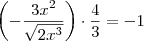 ;
;
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.