 por beel » Dom Nov 20, 2011 23:04
por beel » Dom Nov 20, 2011 23:04
Nessa integrada

tomei o "u" como 2t, assim "du"= 2dt...
substituindo ficou
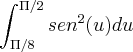
, mas preciso achar
a primitiva de sen²(u) e Deus, como faço isso?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Nov 20, 2011 23:22
por LuizAquino » Dom Nov 20, 2011 23:22
beel escreveu:Nessa integrada
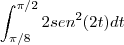
tomei o "u" como 2t, assim "du"= 2dt...
substituindo ficou

(...)
Se você faz a substituição u=2t, então o novo intervalo de integração será
![[\pi/4,\, \pi] [\pi/4,\, \pi]](/latexrender/pictures/75630267086975fcd5d8267076f246c6.png)
. Sendo assim, temos que:

beel escreveu:(..,) mas preciso achar a primitiva de sen²(u) e Deus, como faço isso?
Eu recomendo que você assista a vídeo-aula "31. Cálculo I - Integral de Potências de Seno ou Cosseno". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Ter Nov 22, 2011 14:28
por beel » Ter Nov 22, 2011 14:28
considerei integral de sen²(u) = 1/2 + sen(2u)/4
meu resultado deu
1/2 + sen(pi/2) - sen (pi/2)/4 é isso?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Nov 22, 2011 14:36
por LuizAquino » Ter Nov 22, 2011 14:36
beel escreveu:considerei integral de sen²(u) = 1/2 + sen(2u)/4
meu resultado deu
1/2 + sen(pi/2) - sen (pi/2)/4 é isso?
Para conferir sua resolução, siga os procedimentos abaixo.
Parte 1) Estudar o desenvolvimento de
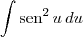
.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (sin(u))^2 du
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução e comparar com a sua.
Parte 2) Calcular o valor de

.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (sin(u))^2 du u=pi/4..pi
- Clique no botão de igual ao lado do campo de entrada.
- Após o processamento irá aparecer o valor dessa integral definida.
- Pronto! Agora basta comparar o valor com o resultado obtido por você.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Seno 1
por estudandoMat » Dom Abr 04, 2010 21:02
- 4 Respostas
- 4734 Exibições
- Última mensagem por estudandoMat

Seg Abr 05, 2010 00:27
Trigonometria
-
- Seno(22,5)°
por estudandoMat » Qua Abr 07, 2010 02:15
- 2 Respostas
- 13000 Exibições
- Última mensagem por estudandoMat

Qua Abr 07, 2010 10:59
Trigonometria
-
- Seno de -?/2
por samra » Sáb Mar 10, 2012 09:34
- 2 Respostas
- 1698 Exibições
- Última mensagem por samra

Sex Mar 30, 2012 00:04
Trigonometria
-
- Limite de seno x
por luiz3107 » Seg Jun 21, 2010 13:55
- 2 Respostas
- 3713 Exibições
- Última mensagem por MarceloFantini

Ter Jun 22, 2010 01:43
Cálculo: Limites, Derivadas e Integrais
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4660 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

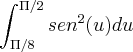 , mas preciso achar
, mas preciso achar

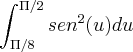 , mas preciso achar
, mas preciso achar
(...)
![[\pi/4,\, \pi] [\pi/4,\, \pi]](/latexrender/pictures/75630267086975fcd5d8267076f246c6.png) . Sendo assim, temos que:
. Sendo assim, temos que:


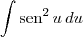 .
. .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)