"determine uma curva
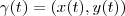 que passe pelo ponto
que passe pelo ponto 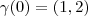 e intercepte ortogonalmente todas as curvas da familia
e intercepte ortogonalmente todas as curvas da familia 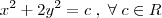 "
"O fato é que eu consegui terminar o exercicio mas nao estou convencido de uma passagem que eu fiz.
em um momento voce se depara igualando o gradiente da função
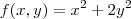 que fica
que fica 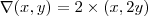 á derivada da função gamma.
á derivada da função gamma.resulta um sistema assim:
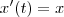
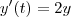
Se voce imagina as variaveis x e y como funções, tudo bem, essas equações diferenciais vão apontar uma exponencial que de fato é a resposta. Mas pra mim elas não são funções. são variaveis do plano real, só. não são funçoes de t.
Não compreendo por que posso tratar o x do lado direito da igualdade como função. Na minha cabeça é só uma incógnita
Estou tendo dificuldade nessa parte da teoria, alguem pode ajudar ? obrigado.


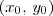 pertence as curvas
pertence as curvas 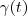 e
e 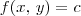 .
.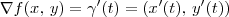 , estamos considerando essa equação em algum ponto
, estamos considerando essa equação em algum ponto 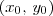 que pertence ao mesmo tempo a
que pertence ao mesmo tempo a 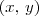 no qual estamos avaliando
no qual estamos avaliando 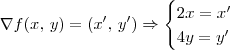

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.