Uma lâmpada está pendurada a 4,5 m de um piso horizontal. Se um homem com 1,80 m de altura caminha afastando-se da luz, com uma velocidade de 1,5 m/s, (A) qual a velocidade de crescimento da sombra? e (B) com que velocidade a ponta da sombra do homem está se movendo?
A figura abaixo ilustra o exercício.
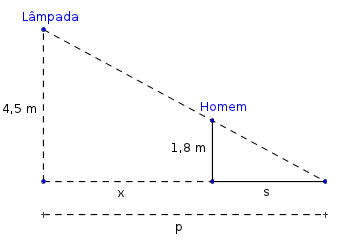
- exercício-taxa-de-variação.png (4.94 KiB) Exibido 8445 vezes
Por semelhança de triângulos, temos que:
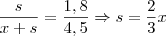
A sombra
s está em função da distância
x, que por sua vez está em função do tempo. Sendo assim, aplicando a Regra da Cadeia:
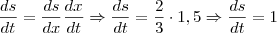
Ou seja, a velocidade de crescimento da sombra é 1 m/s.
Voltando a figura que ilustra o exercício,
p representa a distância percorrida pela "ponta da sombra". Podemos então escrever que:
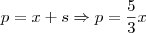
.
O valor de
p está em função de
x, que por sua vez está em função do tempo. Sendo assim, aplicando a Regra da Cadeia:

Ou seja, a velocidade com que a ponta da sombra do homem está se movendo é

m/s.
 A minha resposta pra letra A dá 1 m/s, já a letra B não tenho ideia de como faze-la. Fiz a letra A por semelhança de triangulos, está certo?
A minha resposta pra letra A dá 1 m/s, já a letra B não tenho ideia de como faze-la. Fiz a letra A por semelhança de triangulos, está certo? 

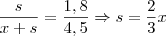
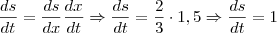
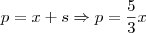 .
.
 m/s.
m/s.