 por TheoFerraz » Sex Out 14, 2011 11:55
por TheoFerraz » Sex Out 14, 2011 11:55
Gente socorro... a prova é segunda e eu percebi que algumas funções que envolvem frações eu não to conseguindo provar a diferenciabilidade pela definição.
Basicamente: prove pela definição que a função
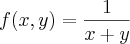
é diferenciável.
Pra começar que eu assumo que o problema nao esteja falando dos ptos (x,0) e (0,y) mas vamo lá
Pela definição, f só é diferenciável

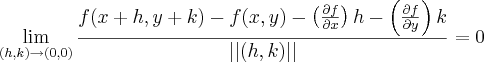
Entao vamos lá. As derivadas parciais são da forma:
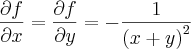
correto ? Então o limite fica assim:
![\lim_{ (h,k)\rightarrow (0,0 } \left[ \left( \frac{1}{x+h+y+k} - \frac{1}{x+y} + \frac{h}{{(x+y)}^{2}} + \frac{k}{{(x+y)}^{2}} \right)\times \frac{1}{||(h,k)||} \right] \lim_{ (h,k)\rightarrow (0,0 } \left[ \left( \frac{1}{x+h+y+k} - \frac{1}{x+y} + \frac{h}{{(x+y)}^{2}} + \frac{k}{{(x+y)}^{2}} \right)\times \frac{1}{||(h,k)||} \right]](/latexrender/pictures/5340638d89d698ebac7734523e3cece1.png)
Na minha cabeça isso ja ta meio errado... Se o limite de uma soma é a soma dos limites entao eu ja poderia distribuir o inverso do modulo em todos esses 4 termos e eu ja obteria limites que não existem. tem coisa errada ai né ?
Muito obrigado! Espero ter ficado claro. Por favor, ajudem-me. Obrigado...
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada pela Definiçao
por PeIdInHu » Sáb Mai 22, 2010 17:24
- 1 Respostas
- 2205 Exibições
- Última mensagem por admin

Sáb Mai 22, 2010 18:24
Cálculo: Limites, Derivadas e Integrais
-
- Integral pela definição
por ARCS » Sáb Abr 09, 2011 15:49
- 1 Respostas
- 1518 Exibições
- Última mensagem por LuizAquino

Dom Abr 10, 2011 13:33
Cálculo: Limites, Derivadas e Integrais
-
- Limite pela definição
por -civil- » Qui Mai 26, 2011 02:37
- 5 Respostas
- 3118 Exibições
- Última mensagem por LuizAquino

Qui Mai 26, 2011 13:31
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definiçao
por tumiattibrz » Sex Mai 27, 2011 17:17
- 3 Respostas
- 2523 Exibições
- Última mensagem por LuizAquino

Sáb Mai 28, 2011 12:28
Cálculo: Limites, Derivadas e Integrais
-
- derivada pela definiçao
por paula luna » Sex Jun 10, 2011 04:41
- 2 Respostas
- 2290 Exibições
- Última mensagem por Fabio Cabral

Sex Jun 10, 2011 11:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
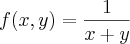 é diferenciável.
é diferenciável.
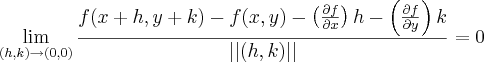
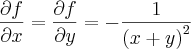 correto ? Então o limite fica assim:
correto ? Então o limite fica assim:![\lim_{ (h,k)\rightarrow (0,0 } \left[ \left( \frac{1}{x+h+y+k} - \frac{1}{x+y} + \frac{h}{{(x+y)}^{2}} + \frac{k}{{(x+y)}^{2}} \right)\times \frac{1}{||(h,k)||} \right] \lim_{ (h,k)\rightarrow (0,0 } \left[ \left( \frac{1}{x+h+y+k} - \frac{1}{x+y} + \frac{h}{{(x+y)}^{2}} + \frac{k}{{(x+y)}^{2}} \right)\times \frac{1}{||(h,k)||} \right]](/latexrender/pictures/5340638d89d698ebac7734523e3cece1.png)

