olá
boa noite
não consigo resolver essas integrais:
?dx/(e^x+e^-x)
?sen(3x)dx/(³?(cos3x)^4)
?dx/(?x*(?x+1))
?ln(x)^3dx/(x)
?x²cos²(x)dx
parece ser trabalhoso, mas por favor quem souber responda a este topico.



vinicius cruz escreveu:
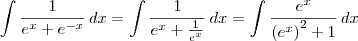
 e
e 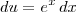 .
.vinicius cruz escreveu:
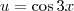 e
e 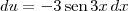 .
.vinicius cruz escreveu:
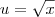 e
e 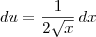 .
.vinicius cruz escreveu:
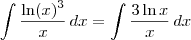
 e
e 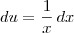 .
.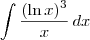 ,
,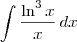 .
. e
e 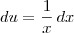 .
.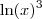 , é tal que
, é tal que 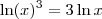 . Já a expressão (ln(x))^3, que pode ser escrita como
. Já a expressão (ln(x))^3, que pode ser escrita como 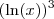 , é tal que
, é tal que 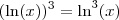 .
.vinicius cruz escreveu:
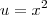 e
e 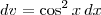 .
.

vinicius cruz escreveu:mas na primeira questão eu não entendi como o "e^x" foi parar em cima ??
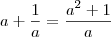 .
.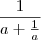 .
.vinicius cruz escreveu:e na segunda questão quais os passos seguintes, pois eu parei em:
2??x/[u*(?x+1)]
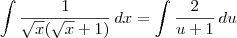


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)