 por theSinister » Dom Ago 14, 2011 17:45
por theSinister » Dom Ago 14, 2011 17:45
vamos considerar a seguinte função :
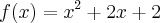
, e queremos encontrar a inclinação da reta tangente a curva no ponto (1,5), ou seja nada mais do q derivar a função , q ficaria
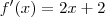
, dai substituímos "x "por "1" e encontramos a inclinação de "4". A partir daí fazemos a equação da reta q ficaria
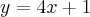
, agora a duvida é: como encontrar o ângulo formado entre a reta e o eixo x? Eu sei q o valor desse ângulo é de 75,9 e a tangente dele é 4, porém não entendi como o meu professor encontrou o valor do angulo . help-me.
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Ago 15, 2011 16:57
por LuizAquino » Seg Ago 15, 2011 16:57
Você precisa usar a função arco tangente, que é a inversa da função tangente.
Você tem que

. Usando uma calculadora científica, obtemos que
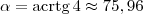
.
Observação1) É comum nas calculadoras científicas aparecer a notação
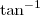
para representar o arco tangente. Portanto, nessas calculadoras você deve digitar

.
2) Sem o uso de calculadora, teríamos que apelar para algum método numérico para calcular
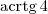
. Por exemplo, o
Método de Newton. Vale lembrar que esses métodos numéricos são estudados na disciplina Cálculo Numérico.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada.Reta tangente á curva
por Blame » Ter Jun 18, 2013 18:32
- 0 Respostas
- 1381 Exibições
- Última mensagem por Blame

Ter Jun 18, 2013 18:32
Cálculo: Limites, Derivadas e Integrais
-
- Calcular reta tangente e normal à curva
por Kingflare » Dom Dez 07, 2014 23:54
- 1 Respostas
- 2695 Exibições
- Última mensagem por Molina

Qua Dez 17, 2014 14:15
Cálculo: Limites, Derivadas e Integrais
-
- Conjuntos intercessão e Conjunto formado pela união
por Fran Ianhez » Ter Set 27, 2016 23:01
- 1 Respostas
- 4407 Exibições
- Última mensagem por Wesleiricardo

Qui Set 27, 2018 22:12
Conjuntos
-
- Calcule a medida do ângulo BNP formado dentro do losango
 por andersontricordiano » Ter Abr 05, 2011 19:07
por andersontricordiano » Ter Abr 05, 2011 19:07
- 1 Respostas
- 4613 Exibições
- Última mensagem por Elcioschin

Ter Abr 05, 2011 19:28
Geometria
-
- Determunar a área limitada pela parábola y= x²+1 e pela reta
por lucat28 » Ter Ago 30, 2011 19:32
- 2 Respostas
- 5105 Exibições
- Última mensagem por lucat28

Dom Set 04, 2011 11:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
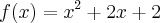 , e queremos encontrar a inclinação da reta tangente a curva no ponto (1,5), ou seja nada mais do q derivar a função , q ficaria
, e queremos encontrar a inclinação da reta tangente a curva no ponto (1,5), ou seja nada mais do q derivar a função , q ficaria 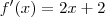 , dai substituímos "x "por "1" e encontramos a inclinação de "4". A partir daí fazemos a equação da reta q ficaria
, dai substituímos "x "por "1" e encontramos a inclinação de "4". A partir daí fazemos a equação da reta q ficaria 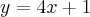 , agora a duvida é: como encontrar o ângulo formado entre a reta e o eixo x? Eu sei q o valor desse ângulo é de 75,9 e a tangente dele é 4, porém não entendi como o meu professor encontrou o valor do angulo . help-me.
, agora a duvida é: como encontrar o ângulo formado entre a reta e o eixo x? Eu sei q o valor desse ângulo é de 75,9 e a tangente dele é 4, porém não entendi como o meu professor encontrou o valor do angulo . help-me.

 . Usando uma calculadora científica, obtemos que
. Usando uma calculadora científica, obtemos que 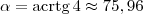 .
.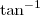 para representar o arco tangente. Portanto, nessas calculadoras você deve digitar
para representar o arco tangente. Portanto, nessas calculadoras você deve digitar  .
.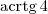 . Por exemplo, o
. Por exemplo, o 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
