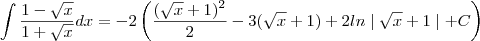-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480135 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 538892 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 502763 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 725620 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2160985 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por pseytow » Qui Nov 27, 2008 21:54
por pseytow » Qui Nov 27, 2008 21:54
existem duas integrais que estou tentando resolver faz algum tempo... infelizmente, sinto que nao estou perto.
se puderem me ajudar, aqui estão:
![\int_{}^{}\frac{\left(x+1 \right)}{\sqrt[2]{x}-1} \int_{}^{}\frac{\left(x+1 \right)}{\sqrt[2]{x}-1}](/latexrender/pictures/88e942f5a46f555a4b99a1cecf19103b.png)
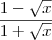
![\int_{}^{}\frac{\left(1-\sqrt[2]{x} \right)}{1+\sqrt[2]{x}} \int_{}^{}\frac{\left(1-\sqrt[2]{x} \right)}{1+\sqrt[2]{x}}](/latexrender/pictures/ec52c70bd1ef534c811c6a3e83bd0694.png)
(tem que ser feitas por substituição)
tranco logo no início:
![u=\sqrt[2]{x}-1 u=\sqrt[2]{x}-1](/latexrender/pictures/2797c0818a97318dc282e12dd49d9faa.png)
![\int_{}^{}\frac{x+1}{2u\sqrt[2]{x}} \int_{}^{}\frac{x+1}{2u\sqrt[2]{x}}](/latexrender/pictures/41433ab6423071ffa9705c2ade8df2ef.png)
nao consigo eliminar o x para poder integrar!
se puderem me indicar o caminho...
obrigado,
pseytow
-
pseytow
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 02, 2008 12:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: cursando
 por Adriano Tavares » Qui Mar 10, 2011 01:52
por Adriano Tavares » Qui Mar 10, 2011 01:52
-
Adriano Tavares
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Mar 07, 2011 16:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em automação industrial
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 7770 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2138 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2236 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 1903 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por Bruhh » Sáb Ago 07, 2010 14:49
- 3 Respostas
- 2888 Exibições
- Última mensagem por Molina

Dom Ago 08, 2010 15:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 41 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{\left(x+1 \right)}{\sqrt[2]{x}-1} \int_{}^{}\frac{\left(x+1 \right)}{\sqrt[2]{x}-1}](/latexrender/pictures/88e942f5a46f555a4b99a1cecf19103b.png)
![\int_{}^{}\frac{\left(1-\sqrt[2]{x} \right)}{1+\sqrt[2]{x}} \int_{}^{}\frac{\left(1-\sqrt[2]{x} \right)}{1+\sqrt[2]{x}}](/latexrender/pictures/ec52c70bd1ef534c811c6a3e83bd0694.png)
![u=\sqrt[2]{x}-1 u=\sqrt[2]{x}-1](/latexrender/pictures/2797c0818a97318dc282e12dd49d9faa.png)
![\int_{}^{}\frac{x+1}{2u\sqrt[2]{x}} \int_{}^{}\frac{x+1}{2u\sqrt[2]{x}}](/latexrender/pictures/41433ab6423071ffa9705c2ade8df2ef.png)

![\int_{}^{}\frac{\left(x+1 \right)}{\sqrt[2]{x}-1} \int_{}^{}\frac{\left(x+1 \right)}{\sqrt[2]{x}-1}](/latexrender/pictures/88e942f5a46f555a4b99a1cecf19103b.png)
![\int_{}^{}\frac{\left(1-\sqrt[2]{x} \right)}{1+\sqrt[2]{x}} \int_{}^{}\frac{\left(1-\sqrt[2]{x} \right)}{1+\sqrt[2]{x}}](/latexrender/pictures/ec52c70bd1ef534c811c6a3e83bd0694.png)
![u=\sqrt[2]{x}-1 u=\sqrt[2]{x}-1](/latexrender/pictures/2797c0818a97318dc282e12dd49d9faa.png)
![\int_{}^{}\frac{x+1}{2u\sqrt[2]{x}} \int_{}^{}\frac{x+1}{2u\sqrt[2]{x}}](/latexrender/pictures/41433ab6423071ffa9705c2ade8df2ef.png)

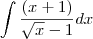
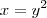 teremos:
teremos: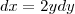
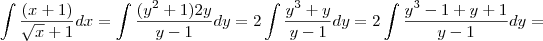
![2\left[\int \frac{y^3-1}{y-1}dy+\int \frac{y+1}{y-1}dy\right]=2\left[\int \frac{(y-1)(y^2+y+1)}{(y-1)}dy+\int \frac{y+1}{y-1}dy\right]= 2\left[\int \frac{y^3-1}{y-1}dy+\int \frac{y+1}{y-1}dy\right]=2\left[\int \frac{(y-1)(y^2+y+1)}{(y-1)}dy+\int \frac{y+1}{y-1}dy\right]=](/latexrender/pictures/f9324182948bec29db8323c2dd8334f5.png)
![2\left[\int (y^2+y+1)dy+\int \frac{y}{y-1}dy +\int \frac{dy}{y-1}\right]= 2\left[\int (y^2+y+1)dy+\int \frac{y}{y-1}dy +\int \frac{dy}{y-1}\right]=](/latexrender/pictures/b4a9008205954de34259621e12498400.png)
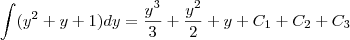
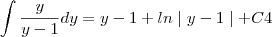
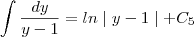
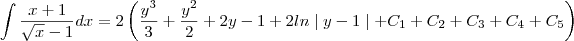
 e substituindo o valor de
e substituindo o valor de  teremos:
teremos: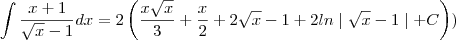
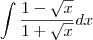
 encontraremos
encontraremos 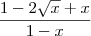
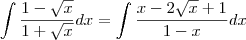
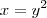 teremos:
teremos: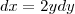
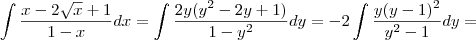

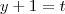 teremos:
teremos: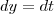
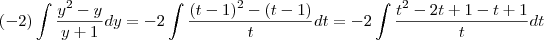
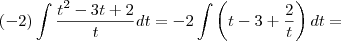
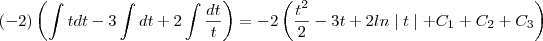
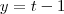 e
e 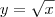 tem-se que
tem-se que 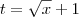

 teremos:
teremos: