-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477821 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529190 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492746 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 698198 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2108059 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por legendkiller2009 » Qui Jun 02, 2011 09:37
por legendkiller2009 » Qui Jun 02, 2011 09:37
Estou a estudar para um exame que vou ter de matemática e não tou a conseguir resolver estas primitivas:
![g(x)=\frac{\sqrt[2]{1+3x}}{x+1} g(x)=\frac{\sqrt[2]{1+3x}}{x+1}](/latexrender/pictures/a7f8745c7240fbe0e5c166bc06ae2bef.png)
![h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[ h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[](/latexrender/pictures/9e4dade81c11385c9aeb59d03e706ccc.png)
Obrigado
-
legendkiller2009
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Jun 01, 2011 19:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por legendkiller2009 » Qui Jun 02, 2011 12:17
por legendkiller2009 » Qui Jun 02, 2011 12:17
ninguem?
-
legendkiller2009
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Jun 01, 2011 19:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por LuizAquino » Qui Jun 02, 2011 15:25
por LuizAquino » Qui Jun 02, 2011 15:25
Qual foi exatamente a sua dificuldade?
Até onde você conseguiu desenvolver?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por legendkiller2009 » Qui Jun 02, 2011 19:36
por legendkiller2009 » Qui Jun 02, 2011 19:36
A segunda já consegui resolver mas a primeira não consigo resolver nem por nada, gostava que alguem me ajuda-se.
-
legendkiller2009
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Jun 01, 2011 19:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por LuizAquino » Qui Jun 02, 2011 20:07
por LuizAquino » Qui Jun 02, 2011 20:07
Você deseja resolver:
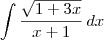
.
Uma maneira é fazer a substituição
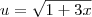
. Note que nesse caso teremos que
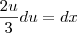
e
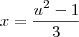
. Portanto, basta resolver:
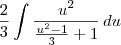
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por legendkiller2009 » Qui Jun 02, 2011 21:26
por legendkiller2009 » Qui Jun 02, 2011 21:26
luiz aquino , vou te ser sincero, não percebi nada do que escreveste.
-
legendkiller2009
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Jun 01, 2011 19:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por LuizAquino » Qui Jun 02, 2011 22:05
por LuizAquino » Qui Jun 02, 2011 22:05
Por definição, dizemos que a função
F é uma primitiva de
f se tivermos que F'(x) = f(x).
Por exemplo, a função F(x) = x³ é uma primitiva de f(x)=3x².
Agora, dada a função
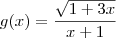
, temos que
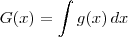
é uma primitiva de
g.
Eu imagino que você já tenha estudado o conteúdo de integral indefinida e a técnica de integração por substituição. Ou não?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [OBM]Estudar para a OBM
por WilsonCarvalho » Qui Jun 16, 2016 22:35
- 0 Respostas
- 3985 Exibições
- Última mensagem por WilsonCarvalho

Qui Jun 16, 2016 22:35
Assuntos Gerais ou OFF-TOPIC
-
- [Derivadas] Exercícios para estudar - ME AJUDEM POR FAVOR
 por Matheus_Silva » Sáb Jun 22, 2013 02:13
por Matheus_Silva » Sáb Jun 22, 2013 02:13
- 0 Respostas
- 2308 Exibições
- Última mensagem por Matheus_Silva

Sáb Jun 22, 2013 02:13
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3106 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
-
- Problemas de exame
por alexpt » Sex Jul 09, 2010 08:40
- 2 Respostas
- 1817 Exibições
- Última mensagem por alexpt

Sex Jul 09, 2010 10:31
Estatística
-
- Exame Nacional
 por joaofonseca » Seg Jun 27, 2011 09:27
por joaofonseca » Seg Jun 27, 2011 09:27
- 2 Respostas
- 3087 Exibições
- Última mensagem por joaofonseca

Seg Jun 27, 2011 18:36
Educação
Usuários navegando neste fórum: Nenhum usuário registrado e 21 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![g(x)=\frac{\sqrt[2]{1+3x}}{x+1} g(x)=\frac{\sqrt[2]{1+3x}}{x+1}](/latexrender/pictures/a7f8745c7240fbe0e5c166bc06ae2bef.png)
![h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[ h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[](/latexrender/pictures/9e4dade81c11385c9aeb59d03e706ccc.png)

![g(x)=\frac{\sqrt[2]{1+3x}}{x+1} g(x)=\frac{\sqrt[2]{1+3x}}{x+1}](/latexrender/pictures/a7f8745c7240fbe0e5c166bc06ae2bef.png)
![h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[ h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[](/latexrender/pictures/9e4dade81c11385c9aeb59d03e706ccc.png)




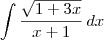 .
.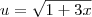 . Note que nesse caso teremos que
. Note que nesse caso teremos que 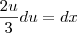 e
e 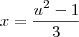 . Portanto, basta resolver:
. Portanto, basta resolver: 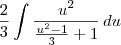 .
.

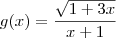 , temos que
, temos que 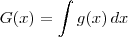 é uma primitiva de g.
é uma primitiva de g.
