-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477742 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528690 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492243 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 696771 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2105585 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Nandodtx » Dom Mai 29, 2011 00:17
por Nandodtx » Dom Mai 29, 2011 00:17
Gente tenho que resolver o seguinte problema:
Um cocho no caso seria isso :
http://www.concrelaje.com.br/imgs/479d7 ... b5efd1.jpgEntao ele ta querendo a inclinação que fornece a maior area do trapezio. Já tentei colocar o valor da base maior e da altura em função do seno do angulo e a/3 mas a função fica mto grande e a derivada mais ainda.
Se alguem tiver alguma dica deixa ai! ^^
Editado pela última vez por
Nandodtx em Dom Mai 29, 2011 14:46, em um total de 1 vez.
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 09:42
por LuizAquino » Dom Mai 29, 2011 09:42
A figura abaixo ilustra o exercício.
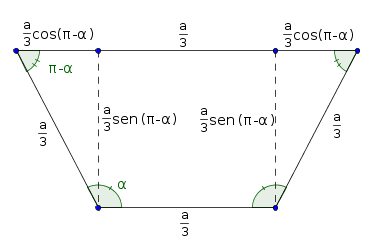
- trapézio.png (8.21 KiB) Exibido 6046 vezes
Você construiu uma figura semelhante?
Note que agora basta montar a função que fornece a área do trapézio em função do ângulo alfa. Vale lembrar que a incógnita
a será uma constante nesse contexto.
Além disso, eu gostaria de frisar que alguns exercícios são naturalmente trabalhosos. Nos problemas de otimização não podemos nos "assustar" com a função ou suas derivadas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Dom Mai 29, 2011 10:12
por Nandodtx » Dom Mai 29, 2011 10:12
Então, a função eu conseguir fazer, mas o problema é que de alguma maneira eu to aplicando a regra da cadeia de forma errada. Não sei se deriva primeiro o produto e depois multiplica pela derivada do seno e do cosseno, ou deriva o sen e cos logo e depois aplica a regra pra produto de derivadas. :S
Editado pela última vez por
Nandodtx em Dom Mai 29, 2011 10:45, em um total de 2 vezes.
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 10:40
por LuizAquino » Dom Mai 29, 2011 10:40
A função para a área terá mais ou menos o formato:
A(x) = f(g(x))h(g(x)).
Desse modo, temos que:
A'(x) = [f(g(x))h(g(x))]' = [f(g(x))]'h(g(x)) + f(g(x))[h(g(x))]' = f'(g(x))g'(x)h(g(x)) + f(g(x))h'(g(x))g'(x).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Dom Mai 29, 2011 10:52
por Nandodtx » Dom Mai 29, 2011 10:52
A função fica assim:
![y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9 y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9](/latexrender/pictures/9a3980c85bb3ac53b51b6f2a657f22c9.png)
Então a derivada seria o primeiro termo derivado multiplicado pelo segundo termo normal e vice-versa no prox, mas dai, no segundo termo fica a derivada de
![[sen(Pi - a).cos(Pi - a) + sen(Pi - a)] ' [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] '](/latexrender/pictures/12b943f403b054b66b44ce694e29cb62.png)
. Dentro dessa derivada tem outro produto, dai fico sem saber como proceder, como aplicar a regra da cadeia corretamente.
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 11:15
por LuizAquino » Dom Mai 29, 2011 11:15
Confira a sua função. Não haverá esse 2 multiplicando toda a expressão.
Note que a sua função está no formato:
A(x) = c[f(g(x))h(g(x)) + f(g(x))].
Isso é o mesmo que:
A(x) = c[h(g(x)) + 1]f(g(x)).
Desse modo, temos que:
A'(x) = c{[h(g(x)) + 1]'f(g(x)) + (h(g(x)) + 1)[f(g(x))]'} = c[h'(g(x))g'(x)f(g(x)) + (h(g(x)) + 1)f'(g(x))g'(x)].
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Dom Mai 29, 2011 12:26
por Nandodtx » Dom Mai 29, 2011 12:26
Cara, valeu meeesmo. Consegui aqui. Deu um pouco de trabalho mais deu certo. A derivada ficou:
![y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1] y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1]](/latexrender/pictures/e9f246146c71692f8a1988c14e27d2a5.png)
Dai fica facil. Resposta final a = 120º
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 12:54
por LuizAquino » Dom Mai 29, 2011 12:54
Confira novamente a função e as suas derivadas.
A função é:
![A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha) A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha)](/latexrender/pictures/385eed659c85df30319fff30056e2eaf.png)
.
Desse modo, temos que:
![A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/05d6154f17c3b98fc1a3f37fea5023df.png)
.
Mas, isso é o mesmo que:
![A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/aba8a17653fa1eb649ba7ae7ee573767.png)
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Dom Mai 29, 2011 14:37
por Nandodtx » Dom Mai 29, 2011 14:37
Realmente, procurei e achei meu erro. Contudo os pontos em que a derivada foi zero são -1 e 1/2 e fazendo o estudo do sinal da função achei que o ponto de max fica no ponto (1/2, F(1/2)). Ajudou muuuiito. Deu pra tirar varias duvidas numa questão só. To começando a vida de universitário agora, to vendo que vo usar mto esse forum aqui.
Show a atenção de vcs com nossas duvidas. Abrçs!
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 20:55
por LuizAquino » Dom Mai 29, 2011 20:55
Na verdade, as raízes da equação
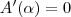
são

e

.
O ponto de máximo é (120°,
A(120°)).
SugestãoEu acredito que os tópicos abaixo podem lhe interessar:
Aulas de Matemática no YouTubeviewtopic.php?f=120&t=3818Curso de Cálculo I no YouTubeviewtopic.php?f=137&t=4280
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Seg Mai 30, 2011 10:22
por Nandodtx » Seg Mai 30, 2011 10:22
é, so que eu fiz cos(Pi-a) = x .Dai o ponto de max vai ser quando x = 1/2 ou x = -1, ou seja, quando alfa for 120º ou 0º
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Seg Mai 30, 2011 11:44
por LuizAquino » Seg Mai 30, 2011 11:44
Vale lembrar que a variável independente original da função é alfa e não x. Por esse motivo que o correto é você dizer que o ponto de máximo ocorre quando alfa = 120°. Note que o fato de você ter feito a substituição "cos(pi - alfa) = x" foi apenas para poder resolver a equação
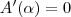
.
Além disso, ao contrário do que você disse, quando alfa = 0° irá ocorrer um ponto de mínimo e não de máximo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicacoes de derivadas
 por aline_n » Qui Jun 02, 2011 17:29
por aline_n » Qui Jun 02, 2011 17:29
- 1 Respostas
- 3463 Exibições
- Última mensagem por LuizAquino

Qui Jun 02, 2011 20:34
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas - Aplicações]
por Scheu » Sex Mar 16, 2012 00:01
- 1 Respostas
- 1575 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 03:17
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivadas
 por lucasabreuo » Seg Mai 06, 2019 11:56
por lucasabreuo » Seg Mai 06, 2019 11:56
- 2 Respostas
- 5051 Exibições
- Última mensagem por adauto martins

Dom Jul 07, 2019 17:07
Cálculo: Limites, Derivadas e Integrais
-
- derivadas e suas aplicações
por ssousa3 » Sex Mai 27, 2011 18:07
- 11 Respostas
- 7555 Exibições
- Última mensagem por ssousa3

Sáb Mai 28, 2011 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicações Derivadas] Dúvida exerc 1
por MrJuniorFerr » Sáb Out 20, 2012 01:21
- 3 Respostas
- 2319 Exibições
- Última mensagem por Russman

Sáb Out 20, 2012 02:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 21 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






![y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9 y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9](/latexrender/pictures/9a3980c85bb3ac53b51b6f2a657f22c9.png)
![[sen(Pi - a).cos(Pi - a) + sen(Pi - a)] ' [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] '](/latexrender/pictures/12b943f403b054b66b44ce694e29cb62.png) . Dentro dessa derivada tem outro produto, dai fico sem saber como proceder, como aplicar a regra da cadeia corretamente.
. Dentro dessa derivada tem outro produto, dai fico sem saber como proceder, como aplicar a regra da cadeia corretamente.

![y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1] y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1]](/latexrender/pictures/e9f246146c71692f8a1988c14e27d2a5.png)

![A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha) A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha)](/latexrender/pictures/385eed659c85df30319fff30056e2eaf.png) .
.![A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/05d6154f17c3b98fc1a3f37fea5023df.png) .
.![A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/aba8a17653fa1eb649ba7ae7ee573767.png) .
.

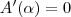 são
são  e
e  .
.

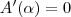 .
.


 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
