Determinar, após exatamente 27 minutos, a taxa de variação da distancia entre os carros e decidir se os mesmo estão se afastando ou aproximando um do outro.R.:-60km/h, ou os carros se aproximam a 60km/h.
Eu queria saber se na hora de montarmos a nossa hipótese seria desse jeito:
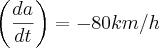 e
e 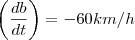
O sinal de menos seria porque os dois carros se aproxima de T, desse modo a distancia deles em relação a T iria diminuir, ou seja, temos uma função decrescente.Correto?
Com isso eu cheguei nessa resposta:
 para t=0,45h, sendo c a hipotenusa do triangulo retangulo formado.
para t=0,45h, sendo c a hipotenusa do triangulo retangulo formado.Só que no enunciado ele fala para decidir se os mesmo estão se afastando ou aproximando um do outro, como a nossa resposta deu -60km/h, não quer dizer que eles estão se aproximando, pois a distancia entre eles diminui.Mas na resposta diz o contrário do meu raciocínio.



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.