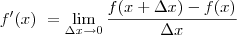-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477779 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528928 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492475 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 697423 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2106740 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Charlys Couto » Sex Abr 29, 2011 12:19
por Charlys Couto » Sex Abr 29, 2011 12:19
Derivar utilizando a de Função ?
Gente eu tenho 2 perguntas para fazer...
1º Onde a gente vai usar a dericada na pratica ?
2º derivar essas funções :
y = x
f(x) = x ao quadrado
f(x) = -x + 1
Ai minha professora pois no quadro como que deve ficar :
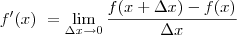
Ai logo depois ela pois um grafico marcando no eixo x a seguinte fração: x . x + DELTA X
Obrigado gente !
-
Charlys Couto
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Abr 29, 2011 12:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Agronomica
- Andamento: cursando
 por Charlys Couto » Sex Abr 29, 2011 13:21
por Charlys Couto » Sex Abr 29, 2011 13:21
Eu tentei aqui em casa e deu o seguinte :
Na 1º questão deu 1
na 2º deu 2x
e na 3º deu -1
ta correto ?
-
Charlys Couto
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Abr 29, 2011 12:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Agronomica
- Andamento: cursando
 por MarceloFantini » Sex Abr 29, 2011 13:26
por MarceloFantini » Sex Abr 29, 2011 13:26
Sim, estão corretas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Charlys Couto » Sex Abr 29, 2011 13:28
por Charlys Couto » Sex Abr 29, 2011 13:28
Obrigado...
-
Charlys Couto
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Abr 29, 2011 12:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Agronomica
- Andamento: cursando
 por LuizAquino » Sex Abr 29, 2011 18:10
por LuizAquino » Sex Abr 29, 2011 18:10
Olá Charlys Couto,
Eu acredito que os tópicos abaixo possam lhe interessar.
Aulas de Matemática no YouTubeviewtopic.php?f=120&t=3818Curso de Cálculo I no YouTubeviewtopic.php?f=137&t=4280
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Yokotoyota » Qui Fev 04, 2016 04:46
por Yokotoyota » Qui Fev 04, 2016 04:46
????????????, ????? ????????? ? ?????? ????? ??????.
-
Yokotoyota
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Fev 03, 2016 09:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- derivar a função
por SILMARAKNETSCH » Qua Nov 14, 2012 18:21
- 3 Respostas
- 3385 Exibições
- Última mensagem por SILMARAKNETSCH

Qua Nov 14, 2012 21:57
Funções
-
- Derivar uma função
por rcs01 » Qui Abr 30, 2015 09:48
- 0 Respostas
- 1948 Exibições
- Última mensagem por rcs01

Qui Abr 30, 2015 09:48
Cálculo: Limites, Derivadas e Integrais
-
- derivar função com módulo
por amanda costa » Sex Jun 01, 2012 01:10
- 4 Respostas
- 3878 Exibições
- Última mensagem por joaofonseca

Sex Jun 01, 2012 18:49
Cálculo: Limites, Derivadas e Integrais
-
- Como derivar esta função: (x^3 + 7x^2 -8).(2x^-3 + x^-4)
 por fabio carvalho » Dom Mai 29, 2016 01:50
por fabio carvalho » Dom Mai 29, 2016 01:50
- 1 Respostas
- 2418 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 21:43
Cálculo: Limites, Derivadas e Integrais
-
- quais os Passos para derivar essa função
por Netolucena » Seg Nov 05, 2012 20:43
- 2 Respostas
- 7136 Exibições
- Última mensagem por e8group

Seg Nov 05, 2012 21:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 26 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.