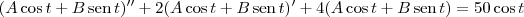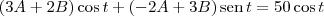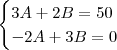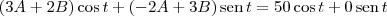por daniel2678 » Qua Abr 27, 2011 02:14
por daniel2678 » Qua Abr 27, 2011 02:14
Gente, estou com problemas para resolver estes exercícios e eles valem nota pra amanhã. Já postei em outros lugares e ninguém conseguiu me fazer entender.
Encontre a carga estacionária e a corrente estacionária em um circuito em
série RCL quando L = 1h, R = 2?, C = 0,25f e E(t) = 50cos(t)V.
e
Ache a carga no capacitor em um circuito em série LRC em t = 0,01s quando
L = 0,05h, R = 2?, C = 0,01f, E(t) = 0V, qo = 5C e i(0) = 0A. Determine a
primeira vez em que a carga sobre o capacitor é igual a zero.
Utilizei a fórmula LQ''+RQ'+Q/C=E(t) no primeiro exercício para chegar em Q"+2Q'+4Q=50cos(t), mas não sei resolver.
O segundo exercício eu só sei a resposta final. Eu estou tentando desde o sábado e nada... É questão de vida ou morte agora... Obrigado!
-
daniel2678
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Abr 27, 2011 01:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Qua Abr 27, 2011 10:59
por LuizAquino » Qua Abr 27, 2011 10:59
Para resolver a equação diferencial Q"+2Q'+4Q=50cos(t), você precisa usar a estratégia de que a função Q(t) tem o formato:
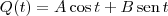
.
O seu objetivo será determinar as constantes A e B. Para isso, comece substituindo a função na equação diferencial:
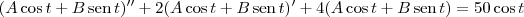
Resolvendo as derivadas e arrumando a equação, você obtém:
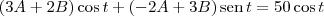
Agora, basta você resolver o sistema:
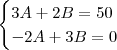 Observação
ObservaçãoPara armar o sistema basta notar que temos a equação:
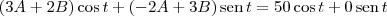
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por 0146251 » Seg Mai 25, 2015 21:42
por 0146251 » Seg Mai 25, 2015 21:42
Ache a carga no capacitor em um circuito em série LRC em t = 0,01s quando
L = 0,05h, R = 2?, C = 0,01f, E(t) = 0V, qo = 5C e i(0) = 0A. Determine a
primeira vez em que a carga sobre o capacitor é igual a zero.
Conforme a equação acima e faço pela equações lineares com coeficientes contantes.
Então tenho a equação:
0,05d²/dt² + 2 dq/dt + 1/0,01q = 0
então obtenho o resultado e para descobrir c1 e c2 faço q(0)=5 e q'(0)=0
Obtendo então c1 e c2, altero apenas o t pelo 0,01s.
Está correto esse raciocínio ?
-
0146251
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Mai 25, 2015 21:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações Diferenciais] De segunda ordem
por palliativos » Dom Nov 16, 2014 20:35
- 1 Respostas
- 1432 Exibições
- Última mensagem por adauto martins

Qua Nov 19, 2014 12:06
Cálculo: Limites, Derivadas e Integrais
-
- Equações Diferenciais-Redução de Ordem uma ajudinha=)
por Garota nerd » Dom Nov 25, 2012 23:59
- 2 Respostas
- 1952 Exibições
- Última mensagem por Garota nerd

Seg Nov 26, 2012 23:32
Cálculo: Limites, Derivadas e Integrais
-
- Equações diferenciais: ordem, tipo e grau
 por luanavsr » Qui Set 05, 2013 14:56
por luanavsr » Qui Set 05, 2013 14:56
- 0 Respostas
- 1339 Exibições
- Última mensagem por luanavsr

Qui Set 05, 2013 14:56
Cálculo: Limites, Derivadas e Integrais
-
- [EDO de 1º ordem] duvida
por CarolMarques » Ter Abr 23, 2013 10:53
- 1 Respostas
- 3026 Exibições
- Última mensagem por young_jedi

Qui Abr 25, 2013 22:38
Cálculo: Limites, Derivadas e Integrais
-
- duvida para derivar a segunda ordem
por PORTER » Ter Nov 04, 2014 21:37
- 3 Respostas
- 3261 Exibições
- Última mensagem por Russman

Qua Nov 05, 2014 11:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


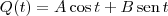 .
.