 por genicleide » Qua Abr 20, 2011 14:28
por genicleide » Qua Abr 20, 2011 14:28
Não estou conseguindo derivar:
![f(x)=\frac{2x}{\sqrt[2]{3x-1}} f(x)=\frac{2x}{\sqrt[2]{3x-1}}](/latexrender/pictures/8827474e2ce86af38df41d6a94a36ec0.png)
Alguém poderia me ajudar, estou tentando pela regra do quociente mas não tá dando certo.
-
genicleide
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Abr 20, 2011 11:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Quimica
- Andamento: cursando
 por LuizAquino » Qua Abr 20, 2011 15:34
por LuizAquino » Qua Abr 20, 2011 15:34
Após aplicar a regra do quociente, será necessário aplicar a regra da cadeia para derivar o termo

:
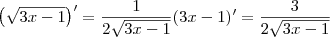
Use essa informação para terminar o exercício. Se não conseguir terminar, envie a sua resolução para identificarmos os problemas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por genicleide » Qua Abr 20, 2011 17:17
por genicleide » Qua Abr 20, 2011 17:17
Bom eu resolvi até certo ponto mas n sei se estou correta. Esta é a minha resolução:
![f(x)= \frac{2x}{\sqrt[]{3x-1}}
\rightarrow
f(x)= \frac{2x}{{(3x-1)}^{1/2}}\rightarrow
f'(x)=\frac{2(3x-1)^{1/2}-3x(3x-1)^{-1/2}}{({3x-1}^{1/2})^{2}}\rightarrow f(x)= \frac{2x}{\sqrt[]{3x-1}}
\rightarrow
f(x)= \frac{2x}{{(3x-1)}^{1/2}}\rightarrow
f'(x)=\frac{2(3x-1)^{1/2}-3x(3x-1)^{-1/2}}{({3x-1}^{1/2})^{2}}\rightarrow](/latexrender/pictures/e6d49b3594b07f2fdf5735b99ba46033.png)
Apartir daki não consigo desenvolver.
Se puder me ajudar
-
genicleide
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Abr 20, 2011 11:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Quimica
- Andamento: cursando
 por LuizAquino » Qua Abr 20, 2011 17:42
por LuizAquino » Qua Abr 20, 2011 17:42
Temos a função
![f(x)= \frac{2x}{\sqrt[]{3x-1}} f(x)= \frac{2x}{\sqrt[]{3x-1}}](/latexrender/pictures/7db572b1ce80bcd4e3cc063a255d7572.png)
. A sua derivada será:
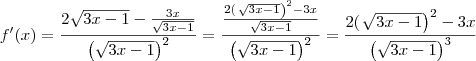
Como o domínio da função é

, temos que
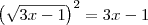
. Desse modo, teremos que:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por genicleide » Qua Abr 20, 2011 19:44
por genicleide » Qua Abr 20, 2011 19:44
Muito obrigada!
-
genicleide
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Abr 20, 2011 11:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Quimica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADAS] Regra da Cadeia
por pauloguerche » Qua Set 07, 2011 17:19
- 4 Respostas
- 4094 Exibições
- Última mensagem por LuizAquino

Qui Set 08, 2011 10:50
Cálculo: Limites, Derivadas e Integrais
-
- [derivadas] regra da cadeia
por emsbp » Sex Mar 16, 2012 08:45
- 2 Respostas
- 2285 Exibições
- Última mensagem por emsbp

Sex Mar 16, 2012 18:38
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADAS] Regra Da Cadeia
por guigoraphael » Qua Ago 07, 2013 21:17
- 0 Respostas
- 1383 Exibições
- Última mensagem por guigoraphael

Qua Ago 07, 2013 21:17
Cálculo: Limites, Derivadas e Integrais
-
- Regra da cadeia para derivadas parciais
por Maisa_Rany » Qua Nov 07, 2018 16:47
- 2 Respostas
- 9481 Exibições
- Última mensagem por Maisa_Rany

Qui Nov 08, 2018 16:33
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2] Regra da cadeia em derivadas parciais
 por NavegantePI » Sáb Jun 25, 2016 18:05
por NavegantePI » Sáb Jun 25, 2016 18:05
- 0 Respostas
- 1990 Exibições
- Última mensagem por NavegantePI

Sáb Jun 25, 2016 18:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=\frac{2x}{\sqrt[2]{3x-1}} f(x)=\frac{2x}{\sqrt[2]{3x-1}}](/latexrender/pictures/8827474e2ce86af38df41d6a94a36ec0.png)

![f(x)=\frac{2x}{\sqrt[2]{3x-1}} f(x)=\frac{2x}{\sqrt[2]{3x-1}}](/latexrender/pictures/8827474e2ce86af38df41d6a94a36ec0.png)

 :
: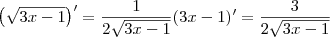

![f(x)= \frac{2x}{\sqrt[]{3x-1}}
\rightarrow
f(x)= \frac{2x}{{(3x-1)}^{1/2}}\rightarrow
f'(x)=\frac{2(3x-1)^{1/2}-3x(3x-1)^{-1/2}}{({3x-1}^{1/2})^{2}}\rightarrow f(x)= \frac{2x}{\sqrt[]{3x-1}}
\rightarrow
f(x)= \frac{2x}{{(3x-1)}^{1/2}}\rightarrow
f'(x)=\frac{2(3x-1)^{1/2}-3x(3x-1)^{-1/2}}{({3x-1}^{1/2})^{2}}\rightarrow](/latexrender/pictures/e6d49b3594b07f2fdf5735b99ba46033.png)

![f(x)= \frac{2x}{\sqrt[]{3x-1}} f(x)= \frac{2x}{\sqrt[]{3x-1}}](/latexrender/pictures/7db572b1ce80bcd4e3cc063a255d7572.png) . A sua derivada será:
. A sua derivada será: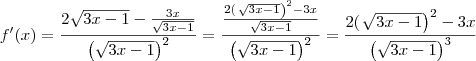
 , temos que
, temos que 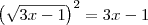 . Desse modo, teremos que:
. Desse modo, teremos que: .
.
